题目内容
12.如图甲所示,足够长度的斜面倾角θ=30°,今在该斜面上放置一质量为m=0.8kg的物体,它收到沿斜面方向的力F作用,力F随时间变化的规律如图乙所示(图中纵坐标是F与mg的比值,现定力沿斜面方向向上为正)已知此物体与斜面间的动摩擦因数μ=$\frac{\sqrt{3}}{6}$,在t=0时物体处于静止状态,g取10m/s2,求:
(1)6s末物体的速度.
(2)6s内力F对物体所做的功.
(3)6s内摩擦力的冲量.
分析 根据牛顿第二定律得出物体运动的加速度,根据加速度与速度的方向关系判断物体的运动,若加速度与速度方向同向,做加速直线运动,若加速度方向与速度方向相反,则做减速运动.根据速度公式求解速度,根据恒力做功表达式求解功,根据冲量的定义求解冲量.
解答 解:(1)0-2s内:
F-mgsin30°=0.1mg<fm=μmgcos30°=0.25mg
故物体保持静止;
2s~4s末:
mgsinθ-fm=ma2
解得:a2=2.5m/s2
根据速度时间关系公式:
v2=a2t2=2.5×2=5m/s
4s~6s末:
mgsinθ+F3-fm=ma3
解得:a3=8.5m/s2
根据速度时间关系公式:
v3=v2+a3t3=5+8.5×2=22m/s
根据位移时间关系公式:
x3=v2t3+$\frac{1}{2}$${a}_{3}{t}_{3}^{2}$=$5×2+\frac{1}{2}×8.5×{2}^{2}$=27m
故3s末物体的速度为22m/s;
(2)6s内F对物体做的功:
W=F3x3=0.6mg×27=0.6×0.8×10×27=129.6J
(3)由分析知:
0~2s内,摩擦力f1=0.1mg,方向沿斜面向上
故冲量:I1=f1t1=0.1×0.8×10×2=1.6N•s
2s~6s内,摩擦力f2=0.25mg,方向沿着斜面向上
故冲量:I2=f2t2=0.25×0.8×10×4=8N•s
故3s内摩擦力的冲量为:
故:I=I1+I2=9.6N•s 方向沿着斜面向上
答:(1)6s末物体的速度为22m/s.
(2)6s内力F对物体所做的功129.6J.
(3)6s内摩擦力的冲量为9.6N•s.
点评 本题关键是受力分析后根据牛顿第二定律判断运动情况,然后结合运动学公式求解各个时间点的速度和位移,最后根据冲量的定义求解冲量.

 如图所示,在一水平、固定的闭合导体圆环上方.有一条形磁铁(N极朝上,S极朝下)由静止开始下落,磁铁从圆环中穿过且不与圆环接触,下列说法正确的是( )
如图所示,在一水平、固定的闭合导体圆环上方.有一条形磁铁(N极朝上,S极朝下)由静止开始下落,磁铁从圆环中穿过且不与圆环接触,下列说法正确的是( )| A. | 圆环中感应电流的方向(从上向下看),先顺时针后逆时针 | |
| B. | 圆环中感应电流的方向(从上向下看),先逆时针后顺时针 | |
| C. | 条形磁铁在下落过程中的加速度始终大于重力加速度g | |
| D. | 条形磁铁在下落过程中动能的增加量等于其重力势能的减少量 |
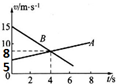
| A. | 在0至4s内A、B两物体运动方向相反 | |
| B. | 在4S时A、B两物体相遇 | |
| C. | t=4s时,A、B两物体的速度大小相等,方向相同 | |
| D. | A做匀加速直线运动,B做匀减速直线运动 |
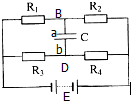 如图所示,已知电源电动势E=12V,内阻不计,电容器德 电容C=1μF,R1:R2:R3:R4=1:2:6:3,则电容器a极板所带电荷量( )
如图所示,已知电源电动势E=12V,内阻不计,电容器德 电容C=1μF,R1:R2:R3:R4=1:2:6:3,则电容器a极板所带电荷量( )| A. | -8×10-6C | B. | 4×10-6C | C. | -4×10-6C | D. | 8×10-6C |
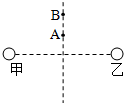 如图所示,甲、乙为两个固定的等量点电荷,A、B为甲、乙连线中垂线上的亮点,将一点电荷q由A点释放,它将沿中垂线向B点运动,下列说法正确的是( )
如图所示,甲、乙为两个固定的等量点电荷,A、B为甲、乙连线中垂线上的亮点,将一点电荷q由A点释放,它将沿中垂线向B点运动,下列说法正确的是( )| A. | 甲、乙一定带同种电荷 | B. | A点的场强一定大于B点的场强 | ||
| C. | A点的电势一定高于B点的电势 | D. | 电荷q的电势能一定减小 |
| A. | 10:1 | B. | 1:10 | C. | 1:1 | D. | 100:1 |
| A. | 不做功 | B. | 做正功 | C. | 做负功 | D. | 不能判定 |
 如图所示,顶角为直角、质量为M的斜面体ABC放在粗糙的水平面上,∠A=30°,现沿垂直于BC方向对斜面体施加力F,斜面体仍保持静止状态.已知重力加速度为g,求斜面体受到的支持力N和摩擦力f.
如图所示,顶角为直角、质量为M的斜面体ABC放在粗糙的水平面上,∠A=30°,现沿垂直于BC方向对斜面体施加力F,斜面体仍保持静止状态.已知重力加速度为g,求斜面体受到的支持力N和摩擦力f. 如图所示是一个模拟风洞中的实验,空气压缩机在风洞可形成竖直向上的均匀气流,将一质量m=2kg的圆球套在与水平面成37°角的细直杆上,直杆固定不动,球内壁与杆间动摩擦因数μ=0.5,将此装置置于风洞中,气流可对球施加竖直向上的恒力F,某时刻由静止释放小球,经t=1s,小球通过的位移为S=0.5m.取g=10m/s2,sin37°=0.6,cos37°=0.8.
如图所示是一个模拟风洞中的实验,空气压缩机在风洞可形成竖直向上的均匀气流,将一质量m=2kg的圆球套在与水平面成37°角的细直杆上,直杆固定不动,球内壁与杆间动摩擦因数μ=0.5,将此装置置于风洞中,气流可对球施加竖直向上的恒力F,某时刻由静止释放小球,经t=1s,小球通过的位移为S=0.5m.取g=10m/s2,sin37°=0.6,cos37°=0.8.