题目内容
1.某河流速度大小为5m/s,一小船在静水中的速度大小是4m/s,已知河宽为120m.为了使船过河的位移最短,船头方向与下游应成多少度?最短位移是多大?分析 画出图象,表示出船在静水中的速度、水速和船的实际速度之间的关系,几何几何图形,利用结合知识即可得出船头与河水的角度和船的最短位移.
解答  解:因船在静水中的速度小于河水的速度,为了使船过河的位移最短,船在静水中的速度方向应与合速度额方向垂直,如图所示:
解:因船在静水中的速度小于河水的速度,为了使船过河的位移最短,船在静水中的速度方向应与合速度额方向垂直,如图所示:
因v水=5m/s,v船=4m/s,由几何关系可得船的合速度为:
v=3m/s
船头方向与上游应成的角度为:α=arccos$\frac{4}{5}$=53°
所以船头方向与下游应成的加速度为:θ=α+90°=143°
船的最短位移为:x=$\frac{d}{cosα}$=$\frac{120}{\frac{4}{5}}$=150m
答:船头方向与下游应成53°角,最短位移是150m
点评 关于渡河问题,是考试的一个热点,要注意分析渡河的几种情况,一是以最短时间渡河的情况,也就是沿垂直于河岸的方向上的速度最大时,渡河时间最短,此时的渡河距离不一定是最短的;二是垂直渡河的情况,要在沿河岸方向上合速度为零,此时要有条件船在静水中速度要大于河流的速度;三是当船在静水中的速度小于河水的流速时,船头的方向垂直于合速度方向,此种情况下对河位移有最小值;再者是当河水的流速发生变化时,对渡河的影响的分析.

练习册系列答案
相关题目
6.一行星绕恒星做圆周运动,由天文观测可得,其运动周期T,速度为V,引力常量为G,则( )
| A. | 恒星的质量为$\frac{{V}^{3}T}{2πG}$ | B. | 行星运动的轨道半径$\frac{VT}{2πG}$ | ||
| C. | 行星的质量为$\frac{2{π}^{2}{V}^{3}}{G{T}^{2}}$ | D. | 行星运动的加速度为$\frac{2πV}{GT}$ |
10. 如图所示,表面粗糙的物体A靠在粗糙的竖直墙面上,在力F的作用下,A、B保持静止,则下列说法正确的是( )
如图所示,表面粗糙的物体A靠在粗糙的竖直墙面上,在力F的作用下,A、B保持静止,则下列说法正确的是( )
 如图所示,表面粗糙的物体A靠在粗糙的竖直墙面上,在力F的作用下,A、B保持静止,则下列说法正确的是( )
如图所示,表面粗糙的物体A靠在粗糙的竖直墙面上,在力F的作用下,A、B保持静止,则下列说法正确的是( )| A. | 物体A受5个力 | B. | 物体A受4个力 | C. | 物体B受4个力 | D. | 物体B受3个力 |
 在如图所示的空间内有竖直向下的有界匀强电场,有界电场的宽度为d,在匀强电场两侧区域内有垂直纸面向里的匀强磁场,其中左侧磁场的磁感应强度未知,右侧磁场的磁感应强度为B.现有一质量为m、电荷量为q的带电正电粒子,从电场左边界的A点以速度v0垂直电场方向射入匀强电场中,粒子的在第一次离开电场时,速度方向与边界的夹角为45°,且粒子在左、右侧磁场中第一次运动时的轨道半径相等,求:
在如图所示的空间内有竖直向下的有界匀强电场,有界电场的宽度为d,在匀强电场两侧区域内有垂直纸面向里的匀强磁场,其中左侧磁场的磁感应强度未知,右侧磁场的磁感应强度为B.现有一质量为m、电荷量为q的带电正电粒子,从电场左边界的A点以速度v0垂直电场方向射入匀强电场中,粒子的在第一次离开电场时,速度方向与边界的夹角为45°,且粒子在左、右侧磁场中第一次运动时的轨道半径相等,求: :量程Ig=500μA,内阻Rg=100Ω
:量程Ig=500μA,内阻Rg=100Ω
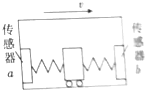 在矩形箱子的前、后壁上各装一个压力传感器,再用两根相同的轻弹簧夹着一个可无摩擦滑动的质量为1.0kg的滑块,两弹簧的另一端分别压在传感器a、b上,其压力大小可直接由传感器读出,如图所示.此装置可以测量汽车的加速度.现将它沿运动方向固定在汽车上,传感器b在前,传感器a在后.已知汽车静止时,传感器a、b的示数均为10N,取g=10m/s2.
在矩形箱子的前、后壁上各装一个压力传感器,再用两根相同的轻弹簧夹着一个可无摩擦滑动的质量为1.0kg的滑块,两弹簧的另一端分别压在传感器a、b上,其压力大小可直接由传感器读出,如图所示.此装置可以测量汽车的加速度.现将它沿运动方向固定在汽车上,传感器b在前,传感器a在后.已知汽车静止时,传感器a、b的示数均为10N,取g=10m/s2. 如图所示的正方形区域,在区域内没有磁场的情况下,带电粒子(不计重力)以某一初速度从AB边中点垂直于该边方向射入时,穿过此区域的时间为t,若在该区域加一垂直纸面向里的匀强磁场,带电粒子仍从同一位置以同一速度射入,粒子从C点射出.若只有时间t为已知量,根据上述条件
如图所示的正方形区域,在区域内没有磁场的情况下,带电粒子(不计重力)以某一初速度从AB边中点垂直于该边方向射入时,穿过此区域的时间为t,若在该区域加一垂直纸面向里的匀强磁场,带电粒子仍从同一位置以同一速度射入,粒子从C点射出.若只有时间t为已知量,根据上述条件 如图所示,内有a、b两个光滑活塞的圆柱形金属容器,其底面固定在水平地板上,活塞将容器分为A、B两部分,两部分中均盛有温度相同的同种理想气体,平衡时,A、B气体柱的高度分别为hA=10cm,hB=20cm,两活塞的重力均忽略不计,活塞的横截面积S=1.0×10-3m2.现用竖直向上的力F拉活塞a,使其缓慢地向上移动△h=3.0cm时,活塞a、b均恰好处于静止状态,环境温度保持不变,外界大气压强为p0=1.0×105Pa,求:
如图所示,内有a、b两个光滑活塞的圆柱形金属容器,其底面固定在水平地板上,活塞将容器分为A、B两部分,两部分中均盛有温度相同的同种理想气体,平衡时,A、B气体柱的高度分别为hA=10cm,hB=20cm,两活塞的重力均忽略不计,活塞的横截面积S=1.0×10-3m2.现用竖直向上的力F拉活塞a,使其缓慢地向上移动△h=3.0cm时,活塞a、b均恰好处于静止状态,环境温度保持不变,外界大气压强为p0=1.0×105Pa,求: