题目内容
15. 如图所示,光滑水平面上有一质量M的平板车,车的上表面是一段粗糙水平轨道,水平轨道左侧连一半径R的四分之一光滑圆弧轨道,圆弧轨道与水平轨道在点O′处相切.现将一质量m的小物块(可视为质点)从平板车的右端以水平向左的初速度v0滑上平板车,小物块恰能到达圆弧轨道的O′处.求:
如图所示,光滑水平面上有一质量M的平板车,车的上表面是一段粗糙水平轨道,水平轨道左侧连一半径R的四分之一光滑圆弧轨道,圆弧轨道与水平轨道在点O′处相切.现将一质量m的小物块(可视为质点)从平板车的右端以水平向左的初速度v0滑上平板车,小物块恰能到达圆弧轨道的O′处.求:(1)小物块到达圆弧轨道的O′处时平板车速度v的大小;
(2)在上述过程中,小物块与平板车组成的系统损失的机械能
(3)要使小物块能到达圆弧轨道的最高点A,小物块进入平板车的速度v'应多大?
分析 (1)平板车和小物块组成的系统动量守恒,小物块恰能到达圆弧轨道的O′处时两者的速度相同,由动量守恒定律求解;
(2)利用能量守恒定律可以求出系统损失的机械能.
(3)小物块恰好能到达圆弧轨道的最高点A时两者的速度相同,根据系统水平方向动量守恒和能量守恒列式,可求得小物块进入平板车的速度v'.
解答 解:(1)平板车和小物块组成的系统动量守恒,取水平向左为正方向,由动量守恒定律得
mv0=(M+m)v
得 v=$\frac{m}{M+m}$v0.
(2)小物块与平板车组成的系统损失的机械能为
△E=$\frac{1}{2}$mv02-$\frac{1}{2}$(M+m)v2=$\frac{mM{v}_{0}^{2}}{2(M+m)}$
(3)平板车和小物块组成的系统在水平方向上动量守恒,设小物块到达圆弧轨道的最高点A时,它们的共同速度为v1
根据动量守恒定律有 mv'=(M+m)v1 ①
根据能量守恒定律有 $\frac{1}{2}$mv'2-$\frac{1}{2}$(M+m)v12=mgR+△E ②
联立解得 v′=$\sqrt{{v}_{0}^{2}+\frac{2(m+M)gR}{M}}$
答:
(1)小物块到达圆弧轨道的O′处时平板车速度v的大小是$\frac{m}{M+m}$v0;
(2)在上述过程中,小物块与平板车组成的系统损失的机械能为$\frac{mM{v}_{0}^{2}}{2(M+m)}$.
(3)要使小物块能到达圆弧轨道的最高点A,小物块进入平板车的速度v'应为$\sqrt{{v}_{0}^{2}+\frac{2(m+M)gR}{M}}$.
点评 本题是系统水平方向动量守恒和能量守恒的问题,要抓住两种情况机械能的损失是相同的,要注意第二种情形系统水平方向动量守恒,但总动量不守恒.

 快乐5加2金卷系列答案
快乐5加2金卷系列答案| A. | 力 | B. | 路程 | C. | 功 | D. | 功率 |
 如图所示,若两颗人造卫星a和b均绕地球做匀速圆周运动,a、b到地心O的距离分别为r1、r2,线速度大小分别为v1、v2,则$\frac{v_1}{v_2}$等于( )
如图所示,若两颗人造卫星a和b均绕地球做匀速圆周运动,a、b到地心O的距离分别为r1、r2,线速度大小分别为v1、v2,则$\frac{v_1}{v_2}$等于( )| A. | $\sqrt{\frac{r_2}{r_1}}$ | B. | $\sqrt{\frac{r_1}{r_2}}$ | C. | $\frac{r_2}{r_1}$ | D. | ${(\frac{r_2}{r_1})^2}$ |

| A. | t1时刻N>G,P有收缩的趋势 | |
| B. | t2时刻N=G,P有扩张的趋势 | |
| C. | t3时刻N=G,此时P中没有感应电流 | |
| D. | t4时刻N<G,此时穿过P的磁通量最小 |
| A. | 月球的质量 | B. | 飞船的质量 | ||
| C. | 月球的密度 | D. | 月球的第一宇宙速度 |
 如图所示,圆弧形轨道AB与BC半径相同且为R,BD为半圆形轨道直径为R.A、C、D处于同一高度,B点可以切换轨道使其平滑连接,其中AB段粗糙,其他轨道光滑,一小球(可视为质点)从A点正上方h处O点自由下落后经轨道ABC,恰好能够到达C点处,再次从O点静止释放小球,则下列说法正确的是( )
如图所示,圆弧形轨道AB与BC半径相同且为R,BD为半圆形轨道直径为R.A、C、D处于同一高度,B点可以切换轨道使其平滑连接,其中AB段粗糙,其他轨道光滑,一小球(可视为质点)从A点正上方h处O点自由下落后经轨道ABC,恰好能够到达C点处,再次从O点静止释放小球,则下列说法正确的是( )| A. | 小球从O到达B过程中,小球的机械能不守恒 | |
| B. | 小球到达B点时,小球动能大小为mg(h+R) | |
| C. | 小球沿ABC到达C点过程中,摩擦力做功大小为mgh | |
| D. | 小球经ABD轨道,能够到达D点 |
| A. | 输电线上损失的功率为△P=$\frac{{U}^{2}}{r}$,U为输电电压,r为输电线的电阻 | |
| B. | 输电线上输送的电流大小为2.0×105 A | |
| C. | 输电线上由电阻造成的损失电压为15 kV | |
| D. | 若改用5 kV电压输电,则输电线上损失的功率为9×108 kW |
 如图所示,用大小为8.0N的水平拉力F,使物体由静止开始沿光滑水平面做匀加速直线运动,在2.0s内通过的位移为8.0m,在此过程中,求:
如图所示,用大小为8.0N的水平拉力F,使物体由静止开始沿光滑水平面做匀加速直线运动,在2.0s内通过的位移为8.0m,在此过程中,求: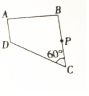 如图为一截面为直角梯形的玻璃砖,其中CD面涂有反光材料,AD⊥AB,BC⊥AB,∠BCD=60°,点P为BC边的中点,BC=d,一细光束沿与AB边垂直的方向射入玻璃砖,经过一次反射和一次折射后,从BC边的点P射出,且射出线与BC边的夹角为30°.已知光在真空中传播的速度大小为c.则该玻璃砖的折射率为$\sqrt{3}$,光束从射入玻璃砖到由点P射出玻璃砖所用的时间为$\frac{5\sqrt{3}d}{4c}$.
如图为一截面为直角梯形的玻璃砖,其中CD面涂有反光材料,AD⊥AB,BC⊥AB,∠BCD=60°,点P为BC边的中点,BC=d,一细光束沿与AB边垂直的方向射入玻璃砖,经过一次反射和一次折射后,从BC边的点P射出,且射出线与BC边的夹角为30°.已知光在真空中传播的速度大小为c.则该玻璃砖的折射率为$\sqrt{3}$,光束从射入玻璃砖到由点P射出玻璃砖所用的时间为$\frac{5\sqrt{3}d}{4c}$.