题目内容
5.设想某登月飞船贴近月球表面绕月球做匀速圆周运动,测得其运动周期为T,飞船在月球上着陆后,航天员利用一摆长为L的单摆做简谐运动,测得单摆振动周期为T0,已知引力常量为G,月球可视为质量分布均匀的球体.根据上述已知条件不能求出的物理量是( )| A. | 月球的质量 | B. | 飞船的质量 | ||
| C. | 月球的密度 | D. | 月球的第一宇宙速度 |
分析 根据万有引力等于重力,列出等式表示出重力加速度.根据万有引力提供向心力,列出等式求出中心天体的质量,从而根据密度公式求解密度,根据第一宇宙速度的定义可求得第一宇宙速度.
解答 解:A、根据T0=2π$\sqrt{\frac{L}{g}}$,知月球表面的重力加速度g=$\frac{4{π}^{2}L}{{T}_{0}^{2}}$,根据万有引力等于重力得,mg=$\frac{GMm}{{R}^{2}}$,$\frac{GMm}{{R}^{2}}$=m$\frac{4{π}^{2}R}{{T}^{2}}$,联立解得M=$\frac{{g}^{3}{T}^{4}}{16{π}^{4}G}$.故A能求出.
B、根据万有引力提供向心力,列出等式中消去飞船的质量,所以无法求出飞船的质量.故B不能求出;
C、根据g=$\frac{4{π}^{2}L}{{T}_{0}^{2}}$,和mg=$\frac{GMm}{{R}^{2}}$可求出月球的半径.根据V=$\frac{4}{3}$πR3可以计算出月球的体积.则根据密度公式即可求得月球的密度,故C能求出;
D、月球的第一宇宙速度是指卫星绕月球表面运行时的速度,则有v=$\sqrt{gR}$,根据以上分析可知,g和R均可以求出,故第一宇宙速度可以求出,故D能求出.
本题选择不能求出的物理量,故选:B.
点评 解决本题的关键掌握万有引力定律的两个重要理论:1、万有引力等于重力,2、万有引力提供向心力,并能灵活运用.同时掌握球体的体积公式的正确应用.

练习册系列答案
 黄冈冠军课课练系列答案
黄冈冠军课课练系列答案
相关题目
10. 如图所示,滑块放在水平地面上,左边受一个弹簧拉力作用,弹簧原长小于悬挂点的高度,水平向右的拉力F拉动滑块,使滑块向右缓慢移动,并且滑块始终没有离开地面,则在上述过程中,下列说法正确的是( )
如图所示,滑块放在水平地面上,左边受一个弹簧拉力作用,弹簧原长小于悬挂点的高度,水平向右的拉力F拉动滑块,使滑块向右缓慢移动,并且滑块始终没有离开地面,则在上述过程中,下列说法正确的是( )
 如图所示,滑块放在水平地面上,左边受一个弹簧拉力作用,弹簧原长小于悬挂点的高度,水平向右的拉力F拉动滑块,使滑块向右缓慢移动,并且滑块始终没有离开地面,则在上述过程中,下列说法正确的是( )
如图所示,滑块放在水平地面上,左边受一个弹簧拉力作用,弹簧原长小于悬挂点的高度,水平向右的拉力F拉动滑块,使滑块向右缓慢移动,并且滑块始终没有离开地面,则在上述过程中,下列说法正确的是( )| A. | 弹簧弹力在竖直方向的分量不变,滑块受到的摩擦力不变 | |
| B. | 弹簧弹力在竖直方向的分量不变,滑块受到的摩擦力变小 | |
| C. | 弹簧弹力在竖直方向的分量增大,滑块受到的摩擦力不变 | |
| D. | 弹簧弹力在竖直方向的分量增大,滑块受到的摩擦力变小 |
11.如图所示,有M和N两颗质量相等的人造地球卫星,都绕地球做匀速圆周运动.两颗卫星相比较( )

| A. | M受到的万有引力较大 | B. | M的周期较小 | ||
| C. | N的线速度较大 | D. | N的角速度较小 |
8.两球A、B在光滑水平面上沿同一直线、同一方向运动,mA=1kg,mB=2kg,vA=6m/s,vB=2m/s.当A追上B并发生碰撞后,两球A、B速度的可能值是( )
| A. | v′A=-1 m/s,v′B=5 m/s | B. | v′A=7 m/s,v′B=1.5 m/s | ||
| C. | v′A=-4 m/s,v′B=7 m/s | D. | v′A=2 m/s,v′B=4 m/s |
17.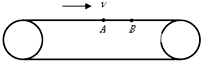 如图所示,传送带以恒定速率v运动,现将质量都是m的小物体甲、乙(视为质点)先后轻放在传送带的最左端,甲到达A处时恰好达到速率v,乙到达B处时恰好达到速率v.在甲、乙两物体在传送带上加速的过程中,下列说法正确的是( )
如图所示,传送带以恒定速率v运动,现将质量都是m的小物体甲、乙(视为质点)先后轻放在传送带的最左端,甲到达A处时恰好达到速率v,乙到达B处时恰好达到速率v.在甲、乙两物体在传送带上加速的过程中,下列说法正确的是( )
 如图所示,传送带以恒定速率v运动,现将质量都是m的小物体甲、乙(视为质点)先后轻放在传送带的最左端,甲到达A处时恰好达到速率v,乙到达B处时恰好达到速率v.在甲、乙两物体在传送带上加速的过程中,下列说法正确的是( )
如图所示,传送带以恒定速率v运动,现将质量都是m的小物体甲、乙(视为质点)先后轻放在传送带的最左端,甲到达A处时恰好达到速率v,乙到达B处时恰好达到速率v.在甲、乙两物体在传送带上加速的过程中,下列说法正确的是( )| A. | 两物体的加速度相同 | |
| B. | 传送带克服摩擦力做的功不相等 | |
| C. | 乙在传送带上滑行系统产生的热量与甲在传送带上滑行系统产生的热量相等 | |
| D. | 传送带对两物体做功不相等 |
14. 用极微弱的可见光做双缝干涉实验,随着时间的增加,在屏上先后出现如图甲、乙、丙所示的图象,则( )
用极微弱的可见光做双缝干涉实验,随着时间的增加,在屏上先后出现如图甲、乙、丙所示的图象,则( )
 用极微弱的可见光做双缝干涉实验,随着时间的增加,在屏上先后出现如图甲、乙、丙所示的图象,则( )
用极微弱的可见光做双缝干涉实验,随着时间的增加,在屏上先后出现如图甲、乙、丙所示的图象,则( )| A. | 图象甲表明光具有粒子性 | |
| B. | 图象丙表明光具有波动性 | |
| C. | 实验表明光是一种概率波 | |
| D. | 在光的干涉条纹中,明条纹是光子能够到达的地方,暗条纹是光子不能到达的地方 |
 如图所示,光滑水平面上有一质量M的平板车,车的上表面是一段粗糙水平轨道,水平轨道左侧连一半径R的四分之一光滑圆弧轨道,圆弧轨道与水平轨道在点O′处相切.现将一质量m的小物块(可视为质点)从平板车的右端以水平向左的初速度v0滑上平板车,小物块恰能到达圆弧轨道的O′处.求:
如图所示,光滑水平面上有一质量M的平板车,车的上表面是一段粗糙水平轨道,水平轨道左侧连一半径R的四分之一光滑圆弧轨道,圆弧轨道与水平轨道在点O′处相切.现将一质量m的小物块(可视为质点)从平板车的右端以水平向左的初速度v0滑上平板车,小物块恰能到达圆弧轨道的O′处.求:
 如图所示,两根足够长、电阻不计的平行金属导轨相距L=0.5m,导轨平面与水平面成θ=37°角,下端连接阻值R=2Ω的电阻.磁感应强度B=0.8T的匀强磁场方向垂直于导轨平面,一根质量为m=0.2kg的导体棒ab放在两导轨上,导体棒ab在导轨之间的有效电阻r=2Ω,棒与导轨垂直并保持良好接触,导体棒与金属导轨间的动摩擦因数μ=0.5,求:
如图所示,两根足够长、电阻不计的平行金属导轨相距L=0.5m,导轨平面与水平面成θ=37°角,下端连接阻值R=2Ω的电阻.磁感应强度B=0.8T的匀强磁场方向垂直于导轨平面,一根质量为m=0.2kg的导体棒ab放在两导轨上,导体棒ab在导轨之间的有效电阻r=2Ω,棒与导轨垂直并保持良好接触,导体棒与金属导轨间的动摩擦因数μ=0.5,求: