题目内容
4. 如图所示,水平光滑导电导轨宽1m,电阻不计,上面垂直于导轨搁有质量为0.2kg、电阻为0.1Ω的导体棒,导轨左端连有一阻值为0.4Ω的电阻R,整个装置处于竖直向下的磁感应强度为0.2T的匀强磁场中,导体棒在外力F=2N作用下,从静止开始运动.求:
如图所示,水平光滑导电导轨宽1m,电阻不计,上面垂直于导轨搁有质量为0.2kg、电阻为0.1Ω的导体棒,导轨左端连有一阻值为0.4Ω的电阻R,整个装置处于竖直向下的磁感应强度为0.2T的匀强磁场中,导体棒在外力F=2N作用下,从静止开始运动.求:(1)导体棒运动的最大加速度.
(2)导体棒匀速运动时的速度.
分析 (1)分析导体棒受力情况,得到加速度最大的状态,然后根据受力分析求得合外力,由牛顿第二定律求得加速度;
(2)由(1)的受力分析,根据匀速运动时受力平衡求解即可.
解答 解:(1)导体棒在水平方向上只受F和安培力${F}_{安}=BIL=\frac{{B}^{2}{L}^{2}v}{R+r}$的作用,那么,当F安=0时,导体棒受到的合外力最大,加速度最大,所以有:
${a}_{m}=\frac{F}{m}=10m/{s}^{2}$;
(2)导体棒匀速运动时受力平衡,由(1)可知:$F={F}_{安}=\frac{{B}^{2}{L}^{2}v}{R+r}$
解得:$v=\frac{F(R+r)}{{B}^{2}{L}^{2}}=25m/s$;
答:(1)导体棒运动的最大加速度为10m/s2;
(2)导体棒匀速运动时的速度为25m/s.
点评 在求解物体运动学问题时,一般要先对物体进行受力分析求得合外力,然后由牛顿第二定律求得加速度,再根据运动学规律求解.

练习册系列答案
相关题目
18. 如图所示,轰炸机沿水平方向以90m/s的速度匀速飞行,到达山坡底端正上方时释放一颗炸弹,并垂直击中山坡上的目标A.已知山坡倾角θ=37°,(g=10m/s2,sin37°=0.6,cos37°=0.8),由此可算出( )
如图所示,轰炸机沿水平方向以90m/s的速度匀速飞行,到达山坡底端正上方时释放一颗炸弹,并垂直击中山坡上的目标A.已知山坡倾角θ=37°,(g=10m/s2,sin37°=0.6,cos37°=0.8),由此可算出( )
 如图所示,轰炸机沿水平方向以90m/s的速度匀速飞行,到达山坡底端正上方时释放一颗炸弹,并垂直击中山坡上的目标A.已知山坡倾角θ=37°,(g=10m/s2,sin37°=0.6,cos37°=0.8),由此可算出( )
如图所示,轰炸机沿水平方向以90m/s的速度匀速飞行,到达山坡底端正上方时释放一颗炸弹,并垂直击中山坡上的目标A.已知山坡倾角θ=37°,(g=10m/s2,sin37°=0.6,cos37°=0.8),由此可算出( )| A. | 炸弹离开飞机后飞行的水平位移为1000m | |
| B. | 炸弹击中A点瞬间的速度与水平方向的夹角为37° | |
| C. | 炸弹离开飞机后的飞行时间为12s | |
| D. | 炸弹离开飞机后飞行的竖直位移为720m |
19.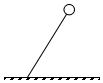 如图所示,在匀强电场中,绝缘丝线一端固定于地面,另一端系住一个带电小球,张紧的丝线使小球处于静止状态.忽略空气阻力,剪断丝线后小球将做( )
如图所示,在匀强电场中,绝缘丝线一端固定于地面,另一端系住一个带电小球,张紧的丝线使小球处于静止状态.忽略空气阻力,剪断丝线后小球将做( )
 如图所示,在匀强电场中,绝缘丝线一端固定于地面,另一端系住一个带电小球,张紧的丝线使小球处于静止状态.忽略空气阻力,剪断丝线后小球将做( )
如图所示,在匀强电场中,绝缘丝线一端固定于地面,另一端系住一个带电小球,张紧的丝线使小球处于静止状态.忽略空气阻力,剪断丝线后小球将做( )| A. | 类平抛运动 | B. | 匀速圆周运动 | C. | 匀加速直线运动 | D. | 变加速曲线运动 |
13.下列核反应中属于α衰变的是( )
| A. | $\underset{11}{5}$B+$\underset{4}{2}$He→$\underset{14}{7}$N+$\underset{1}{0}$n | B. | $\underset{27}{13}$Al+$\underset{2}{1}$H→$\underset{25}{12}$Mg+$\underset{4}{2}$He | ||
| C. | $\underset{230}{90}$Th→$\underset{276}{88}$Ra+$\underset{4}{2}$He | D. | $\underset{3}{1}$H+$\underset{1}{1}$H→$\underset{4}{2}$He |
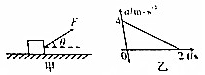 如图甲所示,质量为0.6kg的物块静止在水平面上,物块与水平面间的动摩擦因数为$\frac{1}{3}$,t=0时刻给物块一个与水平方向成θ=37°,斜向右上方的拉力,使物块向右运动,其加速度随时间变化的关系图象如图乙所示,重力加速度为g=10m/s2,sin37°=0.6,cos37°=0.8,求:
如图甲所示,质量为0.6kg的物块静止在水平面上,物块与水平面间的动摩擦因数为$\frac{1}{3}$,t=0时刻给物块一个与水平方向成θ=37°,斜向右上方的拉力,使物块向右运动,其加速度随时间变化的关系图象如图乙所示,重力加速度为g=10m/s2,sin37°=0.6,cos37°=0.8,求: 一倾角为45°的固定绝缘斜面,顶端固定一轻小定滑轮,斜面一侧长度为h的范围内有垂直于斜面向上,磁感应强度大小为B的匀强磁场,如图所示,两细金属棒ab(图中仅标出a端)和cd(图中仅标出c端)长度均为L,质量分别为m和$\frac{\sqrt{2}}{2}$m,用两根不可伸长的柔软轻导线将它们连接成闭合回路abdca,并通过斜面顶端的定滑轮把cd放在斜面上,ab悬空,使两细金属棒ab、cd水平.已知两根导线刚好不在磁场中,每根金属棒的电阻均为R,柔软轻导线电阻不计;金属棒cd与斜面之间的动摩擦因数为0.5.释放金属棒ab,当金属棒ab刚好下落到距离水平面高度为h时,金属棒cd进入磁场区域并刚好做匀速运动.求:
一倾角为45°的固定绝缘斜面,顶端固定一轻小定滑轮,斜面一侧长度为h的范围内有垂直于斜面向上,磁感应强度大小为B的匀强磁场,如图所示,两细金属棒ab(图中仅标出a端)和cd(图中仅标出c端)长度均为L,质量分别为m和$\frac{\sqrt{2}}{2}$m,用两根不可伸长的柔软轻导线将它们连接成闭合回路abdca,并通过斜面顶端的定滑轮把cd放在斜面上,ab悬空,使两细金属棒ab、cd水平.已知两根导线刚好不在磁场中,每根金属棒的电阻均为R,柔软轻导线电阻不计;金属棒cd与斜面之间的动摩擦因数为0.5.释放金属棒ab,当金属棒ab刚好下落到距离水平面高度为h时,金属棒cd进入磁场区域并刚好做匀速运动.求: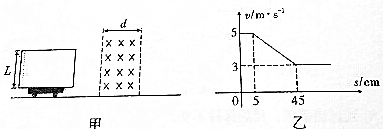
 如图所示,边长为L的正方形导线框abcd以初速度v沿光滑水平面进入宽度为S(S>L)、方向竖直向下与线框平面垂直的匀强有界磁场.如果bc边刚进入磁场时通过导线框的电流强度为i0,则在下列选项所示的四幅反映通过线框电流i随其对O点位移x变化的图象中,可能正确的是( )
如图所示,边长为L的正方形导线框abcd以初速度v沿光滑水平面进入宽度为S(S>L)、方向竖直向下与线框平面垂直的匀强有界磁场.如果bc边刚进入磁场时通过导线框的电流强度为i0,则在下列选项所示的四幅反映通过线框电流i随其对O点位移x变化的图象中,可能正确的是( )



 如图所示,质量M=20kg的物体距离弹簧上端h=2m处自由下落(不计空气阻力,g取10m/s2),将弹簧向下压缩x=2m后向上弹回到原高度.假若在运动过程中的某位置,从物体上脱落了质量m=4kg的一小块,则剩余部分上升的最大高度(相对弹簧上端)可能为( )
如图所示,质量M=20kg的物体距离弹簧上端h=2m处自由下落(不计空气阻力,g取10m/s2),将弹簧向下压缩x=2m后向上弹回到原高度.假若在运动过程中的某位置,从物体上脱落了质量m=4kg的一小块,则剩余部分上升的最大高度(相对弹簧上端)可能为( )