题目内容
7. 一种电流表的原理图如图所示,用两根相同的绝缘轻弹簧将长度L=0.25m的细金属棒MN悬挂起来,两根弹簧的劲度系数均为k=2.0N/m.金属棒MN水平,两弹簧平行且竖直.已知矩形区域abcd内存在匀强磁场,磁感应强度大小B=0.20T,方向垂直纸面向外,且ab长度为0.20m、bc长度为0.05m,与MN的右端N连接的绝缘轻指针可指示标尺上的读数.当金属棒MN中没有电流通过且处于平衡状态时,MN与矩形区域的cd边重合且指针指在标尺上的零刻度线处;当金属棒MN中有电流通过时,指针示数可表示金属棒MN中的电流大小,则关于这个电流表以下说法正确的是( )
一种电流表的原理图如图所示,用两根相同的绝缘轻弹簧将长度L=0.25m的细金属棒MN悬挂起来,两根弹簧的劲度系数均为k=2.0N/m.金属棒MN水平,两弹簧平行且竖直.已知矩形区域abcd内存在匀强磁场,磁感应强度大小B=0.20T,方向垂直纸面向外,且ab长度为0.20m、bc长度为0.05m,与MN的右端N连接的绝缘轻指针可指示标尺上的读数.当金属棒MN中没有电流通过且处于平衡状态时,MN与矩形区域的cd边重合且指针指在标尺上的零刻度线处;当金属棒MN中有电流通过时,指针示数可表示金属棒MN中的电流大小,则关于这个电流表以下说法正确的是( )| A. | 该电流表只能测量由N流向M的电流 | B. | 该电流表只能测量由M流向N的电流 | ||
| C. | 该电流表的量程是0~4.0A | D. | 该电流表的量程是O~5.0A |
分析 当电流表正常工作时,电流表有示数,金属棒将受到向下的安培力,根据左手定则可知MN中电流方向,从而确定MN的哪一端与电源正极相接.
当金属棒处于ab线上时,电流表示数最大,根据平衡条件列出受力平衡方程.扩大量程后根据推导出的平衡方程即可解出正确结果.
解答 解:AB、为使电流表正常工作,作用于通有电流的金属棒MN的安培力必须向下.跟左手定则可知金属棒中电流从M端流向N端.故A错误,B正确;
CD、在cd位置时,重力和弹力平衡,电流越大,MN受到的安培力越大,向下的位移越大,电流最大时,MN与ab重合,MN位移为x,由受力平衡可得:
BILab=kx;
解得:
$\frac{kx}{B{L}_{ab}}=\frac{2×0.05}{0.20×0.20}=2.5A$.
故CD错误.
故选:B.
点评 本题重点要建立好模型,将电流表的量程,与MN的位移建立连接关系,进而由MN的位移x与弹力建立关系,最终在列平衡方程的时候,注意形变量不要用全部的,只用从cd到ab的,这样就把重力避开了.

练习册系列答案
相关题目
17. 如图,表示水平方向的匀强磁场和竖直方向的匀强电场叠加区域,两质点a、b带电荷量均为q,质点B质量是2m,恰好能静止在区域中间,质点A质量是m,恰好能以某一速度沿着垂直于磁场、电场方向做匀速直线运动,且正好与静止的质点b发生正碰,碰后两质点粘合在一起运动,碰撞过程无电荷量损关,则( )
如图,表示水平方向的匀强磁场和竖直方向的匀强电场叠加区域,两质点a、b带电荷量均为q,质点B质量是2m,恰好能静止在区域中间,质点A质量是m,恰好能以某一速度沿着垂直于磁场、电场方向做匀速直线运动,且正好与静止的质点b发生正碰,碰后两质点粘合在一起运动,碰撞过程无电荷量损关,则( )
 如图,表示水平方向的匀强磁场和竖直方向的匀强电场叠加区域,两质点a、b带电荷量均为q,质点B质量是2m,恰好能静止在区域中间,质点A质量是m,恰好能以某一速度沿着垂直于磁场、电场方向做匀速直线运动,且正好与静止的质点b发生正碰,碰后两质点粘合在一起运动,碰撞过程无电荷量损关,则( )
如图,表示水平方向的匀强磁场和竖直方向的匀强电场叠加区域,两质点a、b带电荷量均为q,质点B质量是2m,恰好能静止在区域中间,质点A质量是m,恰好能以某一速度沿着垂直于磁场、电场方向做匀速直线运动,且正好与静止的质点b发生正碰,碰后两质点粘合在一起运动,碰撞过程无电荷量损关,则( )| A. | 两质点均带正电,碰后仍做匀速直线运动 | |
| B. | 两质点均带负电,碰后的运动向上偏且动能增加,电势能减少 | |
| C. | 两质点均带正电,碰后的运动向下偏且动能减少,电势能增加 | |
| D. | 两质点均带负电,碰后的运动向上偏且动能减少,电势能减少 |
18.如图甲所示,一根水平张紧的弹性长绳上有等间距的Q′、P’、O、P、Q质点,相邻两质点间距离为1m,t=0时刻O质点从平衡位置开始沿y轴正方向振动,并产生分别向左、向右传播的简谐横波,O质点振动图象如乙所示,当O点第一次达到正方向最大位移时刻,P点刚开始振动,则下列说法正确的是( )


| A. | 这列波的波长为2m,传播速度为2m/s | |
| B. | 当Q′质点第二次达到正向最大位移时,O质点已经走过35cm路程 | |
| C. | T=3s时,质点P′,P均在平衡位置且均向下运动 | |
| D. | T=2s时,质点P位于波峰,质点P′则位于波谷 |
15. 如图所示,A、B两物体置于水平转台上,并随转台无滑动地绕OO′轴匀速转动,已知A、B到转轴的距离分别为2r和r,则下列说法正确的是( )
如图所示,A、B两物体置于水平转台上,并随转台无滑动地绕OO′轴匀速转动,已知A、B到转轴的距离分别为2r和r,则下列说法正确的是( )
 如图所示,A、B两物体置于水平转台上,并随转台无滑动地绕OO′轴匀速转动,已知A、B到转轴的距离分别为2r和r,则下列说法正确的是( )
如图所示,A、B两物体置于水平转台上,并随转台无滑动地绕OO′轴匀速转动,已知A、B到转轴的距离分别为2r和r,则下列说法正确的是( )| A. | 周期之比TA:TB=1:1 | B. | 线速度之比vA:vB=2:1 | ||
| C. | 转速之比nA:nB=2:1 | D. | 角速度之比ωA:ωB=2:1 |
19.关于力和运动,下列说法正确的是( )
| A. | 某物体所受合力越大,其加速度越大,速度变化越大 | |
| B. | 做直线运动的物体,当运动轨迹变为曲线时,一定受到外力的作用 | |
| C. | 质量不同的两个物体从同一高度自由落下,质量大的物体下落快 | |
| D. | 下落的苹果所受地球的作用力与地球所受太阳的作用力是同种性质的力 |
16. 如图为某款电吹风的电路图,a、b、c、d为四个固定触点.可动的扇形金属触片P可同 时接触两个触点.触片P处于不同位置时,电吹风可处于停机、吹热风和吹冷风等不 同的工作状态.n1和n2分别是理想变压器的两个线圈的匝数.该电吹风的各项参数 如表所示.下列说法正确的有( )
如图为某款电吹风的电路图,a、b、c、d为四个固定触点.可动的扇形金属触片P可同 时接触两个触点.触片P处于不同位置时,电吹风可处于停机、吹热风和吹冷风等不 同的工作状态.n1和n2分别是理想变压器的两个线圈的匝数.该电吹风的各项参数 如表所示.下列说法正确的有( )
 如图为某款电吹风的电路图,a、b、c、d为四个固定触点.可动的扇形金属触片P可同 时接触两个触点.触片P处于不同位置时,电吹风可处于停机、吹热风和吹冷风等不 同的工作状态.n1和n2分别是理想变压器的两个线圈的匝数.该电吹风的各项参数 如表所示.下列说法正确的有( )
如图为某款电吹风的电路图,a、b、c、d为四个固定触点.可动的扇形金属触片P可同 时接触两个触点.触片P处于不同位置时,电吹风可处于停机、吹热风和吹冷风等不 同的工作状态.n1和n2分别是理想变压器的两个线圈的匝数.该电吹风的各项参数 如表所示.下列说法正确的有( )| 热风时输入功率 | 460W |
| 冷风时输入功率 | 60W |
| 小风扇额定电压 | 60W |
| 正常工作时小风扇输出功率 | 52W |
| A. | 吹冷风时触片P与触点b、c接触 | |
| B. | 可由表格中数据计算出小风扇的内阻为60Ω | |
| C. | 变压器原副线圈的匝数比n1:n2=15:55 | |
| D. | 若把电热丝截去一小段后再接入电路,电吹风吹热风时的功率将变小,吹冷风时的 功率不变 |
17.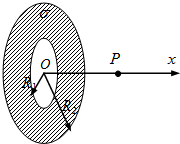 如图,一个内、外半径分别为R1和R2的圆环状均匀带电平面,其单位面积带电量为σ.取环面中心O为原点,以垂直于环面的轴线为x轴.设轴上任意点P到O点的距离为x,P点电场强度的大小为E.下面给出E的四个表达式(式中k为静电力常量),其中只有一个是合理的.你可能不会求解此处的场强E,但是你可以通过一定的物理分析,对下列表达式的合理性做出判断.根据你的判断,E的合理表达式应为( )
如图,一个内、外半径分别为R1和R2的圆环状均匀带电平面,其单位面积带电量为σ.取环面中心O为原点,以垂直于环面的轴线为x轴.设轴上任意点P到O点的距离为x,P点电场强度的大小为E.下面给出E的四个表达式(式中k为静电力常量),其中只有一个是合理的.你可能不会求解此处的场强E,但是你可以通过一定的物理分析,对下列表达式的合理性做出判断.根据你的判断,E的合理表达式应为( )
 如图,一个内、外半径分别为R1和R2的圆环状均匀带电平面,其单位面积带电量为σ.取环面中心O为原点,以垂直于环面的轴线为x轴.设轴上任意点P到O点的距离为x,P点电场强度的大小为E.下面给出E的四个表达式(式中k为静电力常量),其中只有一个是合理的.你可能不会求解此处的场强E,但是你可以通过一定的物理分析,对下列表达式的合理性做出判断.根据你的判断,E的合理表达式应为( )
如图,一个内、外半径分别为R1和R2的圆环状均匀带电平面,其单位面积带电量为σ.取环面中心O为原点,以垂直于环面的轴线为x轴.设轴上任意点P到O点的距离为x,P点电场强度的大小为E.下面给出E的四个表达式(式中k为静电力常量),其中只有一个是合理的.你可能不会求解此处的场强E,但是你可以通过一定的物理分析,对下列表达式的合理性做出判断.根据你的判断,E的合理表达式应为( )| A. | E=2πkσ($\frac{{R}_{1}}{\sqrt{{x}^{2}+{{R}_{1}}^{2}}}$-$\frac{{R}_{2}}{\sqrt{{x}^{2}+{{R}_{2}}^{2}}}$)x | B. | E=2πkσ($\frac{1}{\sqrt{{x}^{2}+{R}_{1}^{2}}}$‐$\frac{1}{\sqrt{{x}^{2}+{R}_{2}^{2}}}$)x | ||
| C. | E=2πkσ($\frac{{R}_{1}}{\sqrt{{x}^{2}+{{{R}_{1}}^{2}}^{\;}}}$+$\frac{{R}_{2}}{\sqrt{{x}^{2}+{R}_{2}^{2}}}$) | D. | E=2πkσ($\frac{1}{\sqrt{{x}^{2}+{R}_{1}^{2}}}$+$\frac{1}{\sqrt{{x}^{2}+{R}_{2}^{2}}}$)x |
 如图所示,在竖直平面内有一条$\frac{1}{4}$圆弧形光滑轨道AB,其半径为R=0.2m,B点的切线方向恰好水平.B点离地面的高度为h=0.45m,一个质量为m=1kg的小滑块,从轨道顶端A点由静止开始沿轨道下滑至B点,然后做平抛运动,落到地面上的C点,不计空气阻力(g取10m/s2),求:
如图所示,在竖直平面内有一条$\frac{1}{4}$圆弧形光滑轨道AB,其半径为R=0.2m,B点的切线方向恰好水平.B点离地面的高度为h=0.45m,一个质量为m=1kg的小滑块,从轨道顶端A点由静止开始沿轨道下滑至B点,然后做平抛运动,落到地面上的C点,不计空气阻力(g取10m/s2),求: