题目内容
1.一根长0.1m的细线,一端系着一个质量为0.18kg的小球,拉住线的另一端,使球在光滑的水平桌面上做匀速圆周运动,当小球的转速增加到原转速3倍时,测得线拉力比原来大40N,此时线突然断裂.求:①线断裂的瞬间,线的拉力;
②线断裂时小球运动的线速度;

③如果桌面高出地面h=0.8m,线断后小球沿垂直于桌边方向飞出.求落地点距桌边的水平距离s.(g取10m/s2)
分析 (1)线末断开前,由线的拉力提供向心力.由题意:小球的转速增加到开始时转速的3倍时细线断开,根据向心力公式可得到线断开时线的拉力与原来拉力的倍数;结合条件:线断开前的瞬间线的拉力比开始时大40N,即可求出线断开前的瞬间,线的拉力大小.
(2)由向心力公式F=m$\frac{{v}^{2}}{R}$求出小球的速度大小.
(3)小球离开桌面后做平抛运动,由高度求出时间,并求出平抛运动的水平位移.
解答 解:(1)设开始时转速为n0,线的拉力为F0,线断开的瞬间的转速为n,线的拉力为F.
由向心力公式F=m(2πn)2R
可得:$\frac{F}{{F{\;}_0}}=\frac{n^2}{{{n_0}^2}}=\frac{9}{1}$
又由题意F=F0+40
得:F=45N
(2)设线断开时速度为v,由公式$F=m\frac{v^2}{R}$ 得:v=5m/s
(3)小球离开桌面后做平抛运动,飞行时间为:$t=\sqrt{\frac{2h}{g}}$=0.4S
水平位移大小:s=vt=5×0.4=2m
答:(1)线断开前的瞬间,线的拉力大小为45N;
(2)线断开的瞬间,小球运动的速度大小为5m/s;
(3)小球飞出后的落地点距桌边AB的水平距离为2m.
点评 对于匀速圆周运动,基本方程是“指向圆心的合力”等于向心力,即F合=Fn,关键分析向心力的来源.

练习册系列答案
 华东师大版一课一练系列答案
华东师大版一课一练系列答案 孟建平名校考卷系列答案
孟建平名校考卷系列答案
相关题目
12. 在研究平抛运动的实验中,让小球多次从斜槽上滚下,在白纸上依次记下小球的位置,某甲和某乙得到的记录纸分别如图所示,从图中明显看出
在研究平抛运动的实验中,让小球多次从斜槽上滚下,在白纸上依次记下小球的位置,某甲和某乙得到的记录纸分别如图所示,从图中明显看出
甲的实验错误是:槽底不水平.
乙的实验错误是:每次释放小球的高度不同.
 在研究平抛运动的实验中,让小球多次从斜槽上滚下,在白纸上依次记下小球的位置,某甲和某乙得到的记录纸分别如图所示,从图中明显看出
在研究平抛运动的实验中,让小球多次从斜槽上滚下,在白纸上依次记下小球的位置,某甲和某乙得到的记录纸分别如图所示,从图中明显看出甲的实验错误是:槽底不水平.
乙的实验错误是:每次释放小球的高度不同.
16. 有一箱鸡蛋在转盘上随转盘以角速度ω做匀速圆周运动,其中一个处于中间位置的鸡蛋质量为m,它(可视为质点)到转轴的距离为R,则其周围鸡蛋对该鸡蛋的作用力大小可表示为( )
有一箱鸡蛋在转盘上随转盘以角速度ω做匀速圆周运动,其中一个处于中间位置的鸡蛋质量为m,它(可视为质点)到转轴的距离为R,则其周围鸡蛋对该鸡蛋的作用力大小可表示为( )
 有一箱鸡蛋在转盘上随转盘以角速度ω做匀速圆周运动,其中一个处于中间位置的鸡蛋质量为m,它(可视为质点)到转轴的距离为R,则其周围鸡蛋对该鸡蛋的作用力大小可表示为( )
有一箱鸡蛋在转盘上随转盘以角速度ω做匀速圆周运动,其中一个处于中间位置的鸡蛋质量为m,它(可视为质点)到转轴的距离为R,则其周围鸡蛋对该鸡蛋的作用力大小可表示为( )| A. | mg | B. | $\sqrt{{m^2}{g^2}+{m^2}{ω^4}{R^2}}$ | ||
| C. | mω2R | D. | $\sqrt{{m^2}{g^2}-{m^2}{ω^4}{R^2}}$ |
6.一个矩形线圈在匀强磁场中转动产生的交流电动势为e=220$\sqrt{2}$sin(100πt) V.关于这个交变电流,下列说法中正确的是( )
| A. | 交变电流的频率为100 Hz | B. | 电动势的有效值为220$\sqrt{2}$V | ||
| C. | 电动势的峰值为311 V | D. | t=0时,线圈平面与中性面垂直 |
11.物体做曲线运动时,其加速度( )
| A. | 可能为0 | B. | 可能不变 | C. | 一定改变 | D. | 一定不变 |
 如图所示,LOO′L′为一折线,它所形成的两个角∠LOO′和∠OO′L′均为45°.折线的右边有一匀强磁场,其方向垂直于纸面向里.一边长为l的正方形导线框沿垂直于OO′的方向以速度v做竖直向上的匀速直线运动,在t=0时刻恰好位于图中所示位置.以逆时针方向为导线框中电流的正方向,在下面四幅图中能够正确表示电流-时间(I-t)关系的是(时间以$\frac{l}{v}$为单位)( )
如图所示,LOO′L′为一折线,它所形成的两个角∠LOO′和∠OO′L′均为45°.折线的右边有一匀强磁场,其方向垂直于纸面向里.一边长为l的正方形导线框沿垂直于OO′的方向以速度v做竖直向上的匀速直线运动,在t=0时刻恰好位于图中所示位置.以逆时针方向为导线框中电流的正方向,在下面四幅图中能够正确表示电流-时间(I-t)关系的是(时间以$\frac{l}{v}$为单位)( )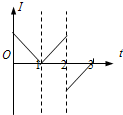



 在海滨游乐场里有一种滑沙的游乐活动.如图所示,人坐在滑板上从斜坡上由静止滑下,滑到斜坡底端B点后进入水平的滑道再滑行一段距离到C点停下.若人和滑板的总质量m=60.0kg,滑板与斜坡滑道和水平滑道间的动摩擦因数均为μ=0.50,斜坡的倾角θ=37°,斜坡与水平滑道间是平滑连接的,整个运动过程中空气阻力忽略不计,重力加速度g取10m/s2,人在斜坡上滑下的距离AB为50m,求人沿水平滑道滑行的最远距离.(sin37°=0.6,cos37°=0.8)
在海滨游乐场里有一种滑沙的游乐活动.如图所示,人坐在滑板上从斜坡上由静止滑下,滑到斜坡底端B点后进入水平的滑道再滑行一段距离到C点停下.若人和滑板的总质量m=60.0kg,滑板与斜坡滑道和水平滑道间的动摩擦因数均为μ=0.50,斜坡的倾角θ=37°,斜坡与水平滑道间是平滑连接的,整个运动过程中空气阻力忽略不计,重力加速度g取10m/s2,人在斜坡上滑下的距离AB为50m,求人沿水平滑道滑行的最远距离.(sin37°=0.6,cos37°=0.8) 如图所示,某同学在做平抛运动的实验时,小球运动过程中先后经历了轨迹(轨迹未画出)上的a、b、c、d四个点;已知图中每个小方格的边长l=1.6cm,g取10m/s2.请你根据小方格纸上的信息,算完成下面的个问题:
如图所示,某同学在做平抛运动的实验时,小球运动过程中先后经历了轨迹(轨迹未画出)上的a、b、c、d四个点;已知图中每个小方格的边长l=1.6cm,g取10m/s2.请你根据小方格纸上的信息,算完成下面的个问题: