题目内容
20. 一个物体沿直线运动,从t=0 时刻开始,物体的$\frac{x}{t}$-t图象如图所示,试请求解物体运动5s后的位移及速度各多少?
一个物体沿直线运动,从t=0 时刻开始,物体的$\frac{x}{t}$-t图象如图所示,试请求解物体运动5s后的位移及速度各多少?
分析 由图象写出$\frac{x}{t}$与t的关系式,对照匀变速直线运动的位移时间公式得到加速度,由图读出初速度,再求5s末物体的速度和5s内的位移.
解答 解:由图得:$\frac{x}{t}$=($\frac{4}{5}$t+4)m/s
由x=v0t+$\frac{1}{2}$at2得:$\frac{x}{t}$=v0+$\frac{1}{2}$at
可得 $\frac{1}{2}$a=$\frac{4}{5}$,a=1.6m/s2.可知,物体的加速度不变,做匀加速直线运动.
图线的纵轴截距表示初速度,则知物体的初速度大小为4m/s.
5s末物体的速度:v=${v}_{0}+at=4+\frac{4}{5}×5=8$m/s
5s内的位移:x=${v}_{0}t+\frac{1}{2}a{t}^{2}=4×5+\frac{1}{2}×\frac{4}{5}×{5}^{2}=30$m
答:物体运动5s后的位移及速度分别是30m和8m/s.
点评 本题关键要运用数学知识得到$\frac{x}{t}$与t的关系式,通过表达式来分析物体的运动情况,不能简单地将$\frac{x}{t}$当作速度瞬时速度进行处理.

练习册系列答案
相关题目
11.图象表示的是甲、乙、丙三个物体相对同一原点的位移图象,在时间t1内,下面说法正确的是( )

| A. | 甲的平均速度最大? | B. | 乙和丙的路程相同? | ||
| C. | 甲的位移最大? | D. | 三者平均速度不相同 |
15. 一质点沿x轴做直线运动,其v-t图象如图所示.质点在t=0时位于x=10m处,开始沿x轴正向运动.当t=8s时,质点在x轴上的位置为( )
一质点沿x轴做直线运动,其v-t图象如图所示.质点在t=0时位于x=10m处,开始沿x轴正向运动.当t=8s时,质点在x轴上的位置为( )
 一质点沿x轴做直线运动,其v-t图象如图所示.质点在t=0时位于x=10m处,开始沿x轴正向运动.当t=8s时,质点在x轴上的位置为( )
一质点沿x轴做直线运动,其v-t图象如图所示.质点在t=0时位于x=10m处,开始沿x轴正向运动.当t=8s时,质点在x轴上的位置为( )| A. | x=3m | B. | x=8m | C. | x=13m | D. | x=4m |
5.作用在同一物体上的两个力,大小分别为6N和9N,其合力大小可能是( )
| A. | 1N | B. | 3N | C. | 13N | D. | 15N |
12.在轻绳的两端各拴一个小球,一个人用手拿着绳子上端的小球,站在三层楼的阳台上,释放小球,使小球自由下落,两小球相继落地的时间差为△t,速度差为△v,如果人站在四层楼的阳台上,同样的方法释放小球,让小球自由下落则两小球相继落地的时间差△t和速度差△v将( )
| A. | △t不变△v变小 | B. | △t变大△v变大 | C. | △t变小△v变大 | D. | △t变小△v变小 |
9.小球由地面竖直上抛,上升的最大高度为H,设所受阻力大小恒定,取地面为零重力势能参考面.在上升至离地高度h处,小球的动能是势能的3倍,在下落至离地高度h处,小球的势能是动能的3倍,则h等于( )
| A. | $\frac{H}{8}$ | B. | $\frac{3H}{8}$ | C. | $\frac{3H}{9}$ | D. | $\frac{4H}{9}$ |
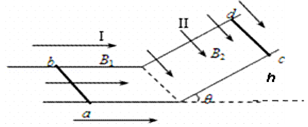 如图所示,倾斜角θ=30°的光滑倾斜导体轨道(足够长)与光滑水平导体轨道连接.轨道宽度均为L=1m,电阻忽略不计.匀强磁场I仅分布在水平轨道平面所在区域,方向水平向右,大小B1=1T;匀强磁场II仅分布在倾斜轨道平面所在区域,方向垂直于倾斜轨道平面向下,大小B2=1T.现将两质量均为m=0.2kg,电阻均为R=0.5Ω的相同导体棒ab和cd,垂直于轨道分别置于水平轨道上和倾斜轨道上,并同时由静止释放.取g=10m/s2.
如图所示,倾斜角θ=30°的光滑倾斜导体轨道(足够长)与光滑水平导体轨道连接.轨道宽度均为L=1m,电阻忽略不计.匀强磁场I仅分布在水平轨道平面所在区域,方向水平向右,大小B1=1T;匀强磁场II仅分布在倾斜轨道平面所在区域,方向垂直于倾斜轨道平面向下,大小B2=1T.现将两质量均为m=0.2kg,电阻均为R=0.5Ω的相同导体棒ab和cd,垂直于轨道分别置于水平轨道上和倾斜轨道上,并同时由静止释放.取g=10m/s2.