题目内容
2. 如图1所示,不计电阻的平行金属导轨竖直放置,导轨间距为L,上端接有电阻R,虚线MN下方是垂直于导轨平面的磁场(图中未画出),同一水平高度各处磁感应强度相同,从虚线MN开始建立竖直向下的坐标轴y(坐标原点O在虚线MN上),磁感应强度B与y关系为:B=B0sin($\frac{π}{d}y$),如图2所示,图中B0、d为已知量,现将质量为m、电阻为r的金属杆ab,从距MN高h处垂直导轨由静止释放,杆下落过程中始终与导轨保持良好接触,重力加速度为g,求:
如图1所示,不计电阻的平行金属导轨竖直放置,导轨间距为L,上端接有电阻R,虚线MN下方是垂直于导轨平面的磁场(图中未画出),同一水平高度各处磁感应强度相同,从虚线MN开始建立竖直向下的坐标轴y(坐标原点O在虚线MN上),磁感应强度B与y关系为:B=B0sin($\frac{π}{d}y$),如图2所示,图中B0、d为已知量,现将质量为m、电阻为r的金属杆ab,从距MN高h处垂直导轨由静止释放,杆下落过程中始终与导轨保持良好接触,重力加速度为g,求:(1)杆自由下落至MN处时速度大小v;
(2)杆从进入磁场开始受变力F作用,竖直向下做匀速直线运动.求:在下降高度2d过程中,变力F所做的功.
分析 (1)根据动能定理,选取杆自由下落至MN处作为过程,即可求解速度大小;
(2)依据功能关系,结合正弦式交流电的有效值等于最大值×$\frac{\sqrt{2}}{2}$,并根据Q=$\frac{{E}^{2}}{R+r}$,即可求解.
解答 解:(1)选取杆自由下落至MN处为过程,根据动能定理,则有:
mgh=$\frac{1}{2}m{v}^{2}-0$
解得:v=$\sqrt{2gh}$;
(2)杆从进入磁场开始受变力F作用,竖直向下做匀速直线运动,且磁感应强度B与y关系为:
B=B0sin($\frac{π}{d}y$),
那么棒产生正弦式交流电,感应电动势为:E=$\frac{\sqrt{2}}{2}{B}_{0}Lv$;
依据功能关系,在下降高度2d过程中,则有:WF=$\frac{{E}^{2}}{R+r}$-mg•2d;
解得:WF=$\frac{{B}_{0}^{2}{L}^{2}gh}{R+r}$-2mgd.
答:(1)杆自由下落至MN处时速度大小$\sqrt{2gh}$;
(2)杆在下降高度2d过程中,变力F所做的功$\frac{{B}_{0}^{2}{L}^{2}gh}{R+r}$-2mgd.
点评 考查动能定理与功能关系的应用,掌握选取过程的重要性,注意力做功的正负值,同时理解正弦式交流电的有效值与最大值的关系.

练习册系列答案
 冲刺100分1号卷系列答案
冲刺100分1号卷系列答案
相关题目
14.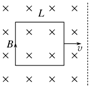 如图所示.边长为L的正方形闭合导线框置于光滑水平面上,有界匀强磁场与水平面垂直.用水平向右的拉力将线框分别以速度v1,v2拉出磁场.下列说法中正确的是( )
如图所示.边长为L的正方形闭合导线框置于光滑水平面上,有界匀强磁场与水平面垂直.用水平向右的拉力将线框分别以速度v1,v2拉出磁场.下列说法中正确的是( )
 如图所示.边长为L的正方形闭合导线框置于光滑水平面上,有界匀强磁场与水平面垂直.用水平向右的拉力将线框分别以速度v1,v2拉出磁场.下列说法中正确的是( )
如图所示.边长为L的正方形闭合导线框置于光滑水平面上,有界匀强磁场与水平面垂直.用水平向右的拉力将线框分别以速度v1,v2拉出磁场.下列说法中正确的是( )| A. | 若v1>v2,则拉力F1>F2 | |
| B. | 若v1>v2,则通过导线框截面的电荷量q1>q2 | |
| C. | 若v1>v2,则拉力的功率P1=2P2 | |
| D. | 若v1>v2,则线框中产生的热量Q1=2Q2 |
 某实验小组设计了如图所示的实验装置探究加速度与力、质量的关系,开始时闭合开关,电磁铁将A、B两个小车吸住,断开开关,两小车同时在细绳拉力作用下在水平桌面沿同一直线相向运动.实验中始终保持小车质量远大于托盘和砝码的质量,实验装置中各部分摩擦阻力可忽略不计.
某实验小组设计了如图所示的实验装置探究加速度与力、质量的关系,开始时闭合开关,电磁铁将A、B两个小车吸住,断开开关,两小车同时在细绳拉力作用下在水平桌面沿同一直线相向运动.实验中始终保持小车质量远大于托盘和砝码的质量,实验装置中各部分摩擦阻力可忽略不计.
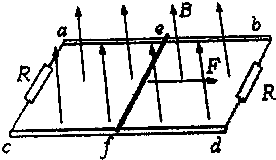 如图所示,两根间距L=1.0m、足够长平行光滑金属导轨ab、cd水平放置,两端均与阻值R=2.0Ω的电阻相连.质量m=0.2kg的导体棒ef在恒定外力F作用下由静止开始运动,导体棒长度与两导轨间距相等,导体棒电阻为r=1.0Ω,整个装置处于垂直于导轨平面向上的匀强磁场B中,导体棒运动过程中与金属导轨接触良好(两导轨及导线电阻不计).求:
如图所示,两根间距L=1.0m、足够长平行光滑金属导轨ab、cd水平放置,两端均与阻值R=2.0Ω的电阻相连.质量m=0.2kg的导体棒ef在恒定外力F作用下由静止开始运动,导体棒长度与两导轨间距相等,导体棒电阻为r=1.0Ω,整个装置处于垂直于导轨平面向上的匀强磁场B中,导体棒运动过程中与金属导轨接触良好(两导轨及导线电阻不计).求: 水平放置的光滑平行金属导轨处于竖直向下的匀强磁场中,导轨的一端接电阻R=1.2Ω,金属棒ab的质量m=0.50kg,电阻r=0.24Ω,在水平恒力F作用下由静止开始向右运动,达到的最大速度v=0.20m/s,电阻R上消耗的最大电功率是P=0.30W.导轨的电阻不计,导轨足够长且与金属棒接触良好.求:
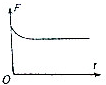
水平放置的光滑平行金属导轨处于竖直向下的匀强磁场中,导轨的一端接电阻R=1.2Ω,金属棒ab的质量m=0.50kg,电阻r=0.24Ω,在水平恒力F作用下由静止开始向右运动,达到的最大速度v=0.20m/s,电阻R上消耗的最大电功率是P=0.30W.导轨的电阻不计,导轨足够长且与金属棒接触良好.求: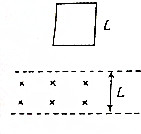 如图所示,间距为L的两水平虚线间存在垂直纸面向里的水平匀强磁场,一边长为L的正方形闭合金属线框自上方某处自由释放,线框平面始终在同一竖直平面内,下边始终水平,以刚进入磁场时为计时起点,则线框所受安培力F大小随时间t变化的关系图线可能为( )
如图所示,间距为L的两水平虚线间存在垂直纸面向里的水平匀强磁场,一边长为L的正方形闭合金属线框自上方某处自由释放,线框平面始终在同一竖直平面内,下边始终水平,以刚进入磁场时为计时起点,则线框所受安培力F大小随时间t变化的关系图线可能为( )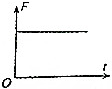


 如图所示,在竖直放置的足够大的铅屏A的右表面上贴着β 射线(即电子)放射源P,已知射线实质为高速电子流,放射源放出β 粒子的速度为v0.足够大的荧光屏M与铅屏A平行放置,相距为d,其间有水平向左的匀强电场,电场强度大小为E.已知电子电量为e,电子质量为m.求:
如图所示,在竖直放置的足够大的铅屏A的右表面上贴着β 射线(即电子)放射源P,已知射线实质为高速电子流,放射源放出β 粒子的速度为v0.足够大的荧光屏M与铅屏A平行放置,相距为d,其间有水平向左的匀强电场,电场强度大小为E.已知电子电量为e,电子质量为m.求: 如图所示,竖直平面直角坐标系中,一半径为R的绝缘光滑管道位于其中,管道圆心坐标为(0,R),其下端点与x轴相切与坐标原点,其上端点与y轴交于C点,坐标为(0,2R).在第二象限内,存在水平向右、范围足够大的匀强电场,电场强度大小为E1=$\frac{\sqrt{3}mg}{3q}$,在x≥R,y≥0范围内,有水平向左,范围足够大的匀强电场,电场强度大小为E1=$\frac{mg}{q}$.现有一与x轴正方向夹角为45°,足够长的绝缘斜面位于第一象限的电场中,斜面底端坐标为(R,0),x轴上0≤x≤R范围内是水平光滑轨道,左端与管道下端相切,右端与斜面底端平滑连接,有一质量为m,带电量为+q的小球,从静止开始,由斜面上某点A下滑,通过水平光滑轨道(不计转角处能量损失),从管道下端点B进入管道(小球直径略小于管道内径,不计小球的电量损失)(已知重力加速度为g).试求:
如图所示,竖直平面直角坐标系中,一半径为R的绝缘光滑管道位于其中,管道圆心坐标为(0,R),其下端点与x轴相切与坐标原点,其上端点与y轴交于C点,坐标为(0,2R).在第二象限内,存在水平向右、范围足够大的匀强电场,电场强度大小为E1=$\frac{\sqrt{3}mg}{3q}$,在x≥R,y≥0范围内,有水平向左,范围足够大的匀强电场,电场强度大小为E1=$\frac{mg}{q}$.现有一与x轴正方向夹角为45°,足够长的绝缘斜面位于第一象限的电场中,斜面底端坐标为(R,0),x轴上0≤x≤R范围内是水平光滑轨道,左端与管道下端相切,右端与斜面底端平滑连接,有一质量为m,带电量为+q的小球,从静止开始,由斜面上某点A下滑,通过水平光滑轨道(不计转角处能量损失),从管道下端点B进入管道(小球直径略小于管道内径,不计小球的电量损失)(已知重力加速度为g).试求: