题目内容
5.如图甲所示,两组平行正对金属薄板AB和CD,CD的左端紧靠B板.B与C、A与D分别连接后,接上如图乙所示规律变化的电压,忽略极板正对部分之外的电场.位于A板中心P处的粒子源可以产生质量为m、电荷量为q的带电粒子,粒子的重力和初速度均可忽略不计.已知t=0时刻产生的粒子,恰好在t=2T0时刻从B板中心的小孔Q处穿过,并在t=3T0时刻从CD板的右端射出.求: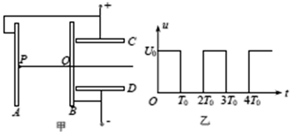
(1)AB板间的距离;
(2)C或D板的长度;
(3)t=$\frac{{T}_{0}}{2}$时刻产生的粒子到达Q点时的速度,比t=0时刻产生的粒子到达Q点时的速度大还是小?请说明理由.
分析 (1)在0~T0时间内,A、B板间存在匀强电场,粒子做匀加速运动,由牛顿第二定律和运动学公式求出粒子运动的位移.在T0~2T0时间内,粒子做匀速运动,结合速度求得粒子前进的距离,从而求得AB板间的距离.
(2)在2T0~3T0时间内,粒子在C、D板间做类平抛运动,C或D板的长度等于水平分位移大小,由位移公式求解.
(3)分析t=$\frac{{T}_{0}}{2}$时刻产生的粒子在A、B板间的运动情况,由位移公式和速度结合求得到达Q点时的速度.
解答 解:(1)在0~T0时间内,A、B板间存在匀强电场,粒子做匀加速运动,由牛顿第二定律得
qE=ma ①
而$E=\frac{U_0}{d}$ ②
位移为 ${x_1}=\frac{1}{2}aT_0^2$ ③
在T0~2T0时间内,粒子做匀速运动,则有 x2=aT0•T0 ④
而x1+x2=d ⑤
整理得,AB板间的距离为 $d=\sqrt{\frac{{3q{U_0}}}{2m}}{T_0}$ ⑥
(2)粒子在C、D板间运动时,沿平行于极板方向做匀速运动,速度为 v1=aT0 ⑦
则C或D板的长度 L=v1T0 ⑧
整理得 $L=\sqrt{\frac{{2q{U_0}}}{3m}}{T_0}$ ⑨
(3)$t=\frac{T_0}{2}$时刻产生的粒子到达Q点时的速度,比t=0时刻产生的粒子到达Q点时的速度大.
方法一:
由(2)知,t=0时刻产生的粒子到达Q点时的速度 v1=aT0 ⑩
$t=\frac{T_0}{2}$时刻产生的粒子先加速$\frac{T_0}{2}$,再匀速运动T0,设又加速时间t到达Q,根据运动学公式得
$\frac{1}{2}a{(\frac{T_0}{2})^2}+a(\frac{T_0}{2}){T_0}+a\frac{T_0}{2}•t+\frac{1}{2}a{t^2}=d$⑪
整理得 $t=\frac{{\sqrt{8}-1}}{2}{T_0}$⑫
因为t<T0,所以此解符合题设条件.
此时粒子的速度大小 ${v_2}=a(\frac{T_0}{2}+t)=\sqrt{2}a{T_0}$⑬
所以v2>v1
方法二: 两种情况下粒子运动的v-t图象如图
两种情况下粒子运动的v-t图象如图
t=0时刻产生的粒子,在t=2T0时刻到达Q点时的速度v1=aT0,v-t图象与t轴围成的“面积”即为A、B板间距离d.
$t=\frac{T_0}{2}$时刻产生的粒子在$t=2{T_0}+\frac{T_0}{2}$时刻的速度为aT0,但此时间内 v-t图象与t轴围成的“面积”小于第一种情况0-2T0时间内的“面积”,所以此时粒子还未到达Q点,仍继续加速.故到达Q点时速度一定大于aT0.
答:
(1)AB板间的距离是$\sqrt{\frac{3q{U}_{0}}{2m}}{T}_{0}$;
(2)C或D板的长度是$\sqrt{\frac{2q{U}_{0}}{3m}}{T}_{0}$;
(3)t=$\frac{{T}_{0}}{2}$时刻产生的粒子到达Q点时的速度比t=0时刻产生的粒子到达Q点时的速度大.
点评 本题中带电粒子在周期性电场中运动问题,分析粒子的运动情况是关键,运用运动的分解法进行研究.

 备战中考寒假系列答案
备战中考寒假系列答案 一质量为1kg的物体从高空由静止下落,下落过程中所受空气阻力恒定,在开始一段时间内其位移x随时间t变化的关系图象如图所示.取g=10m/s2.物体下落过程中所受空气阻力的大小为( )
一质量为1kg的物体从高空由静止下落,下落过程中所受空气阻力恒定,在开始一段时间内其位移x随时间t变化的关系图象如图所示.取g=10m/s2.物体下落过程中所受空气阻力的大小为( )| A. | 1N | B. | 2N | C. | 3N | D. | 4N |
| A. | 电场线既能描述电场强度的方向,也能描述电场强度的强弱 | |
| B. | 电场线是带电粒子在电场中运动的轨迹 | |
| C. | 电场线的疏密程度表明该点的场强大小 | |
| D. | 电场线是客观存在的曲线 |
| A. | 前2s内重力的功率为200W | |
| B. | 前2s内重力的功率为400W | |
| C. | 落地前1s内重力做功与第1s内重力做功相等 | |
| D. | 落地前1s内重力做功比第1s内重力做功多 |
 在一倾角为θ的粗糙斜面上,有一个被水平方向的绳子拉住的静止后的小球,如图所示,若小球质量为m,则绳子的拉力为( )
在一倾角为θ的粗糙斜面上,有一个被水平方向的绳子拉住的静止后的小球,如图所示,若小球质量为m,则绳子的拉力为( )| A. | mgsinθ | B. | mgtanθ | C. | $\frac{mgsinθ}{1+cosθ}$ | D. | $\frac{mg}{cosθ}$ |
 在如图所示宽度范围内,用场强为E的匀强电场可使初速度是v0的某种带正电粒子偏转θ角.在同样宽度范围内,若改用方向垂直于纸面向外的磁感应强度为B的匀强磁场,使该粒子穿过该区域,并使偏转角也为θ(不计粒子的重力),则( )
在如图所示宽度范围内,用场强为E的匀强电场可使初速度是v0的某种带正电粒子偏转θ角.在同样宽度范围内,若改用方向垂直于纸面向外的磁感应强度为B的匀强磁场,使该粒子穿过该区域,并使偏转角也为θ(不计粒子的重力),则( )| A. | 电场强度E与磁感应强度B之比$\frac{E}{B}$=$\frac{{v}_{0}}{sinθ}$ | |
| B. | 电场强度E与磁感应强度B之比$\frac{E}{B}$=$\frac{{v}_{0}}{cosθ}$ | |
| C. | 粒子穿过电场和磁场的时间之比$\frac{{t}_{1}}{{t}_{2}}$=$\frac{sinθ}{θ}$ | |
| D. | 粒子穿过电场和磁场的时间之比$\frac{{t}_{1}}{{t}_{2}}$=$\frac{cosθ}{θ}$ |
 如图所示为一列简谐横波在t=0时刻的波形图,此时x=18m处的质点刚开始振动,t=1.5s时,x=30m处的质点第一次到达波峰,则下列说法正确的是( )
如图所示为一列简谐横波在t=0时刻的波形图,此时x=18m处的质点刚开始振动,t=1.5s时,x=30m处的质点第一次到达波峰,则下列说法正确的是( )| A. | 质点P振动的周期为1.2s | |
| B. | 该波传播速度为10m/s | |
| C. | t=0时刻开始,质点Q比质点P先回到平衡位置 | |
| D. | t=0时刻开始,经$\frac{1}{4}$个周期内,质点Q运动的路程为2cm | |
| E. | t=0.2时,质点Q运动到波峰位置 |
 如图所示,光滑斜面AE被分为四个相等的部分,一物体从A点由静止释放,它沿斜面向下做匀加速运动,依次通过B、C、D点,最后到达底端E点.下列说法正确的是( )
如图所示,光滑斜面AE被分为四个相等的部分,一物体从A点由静止释放,它沿斜面向下做匀加速运动,依次通过B、C、D点,最后到达底端E点.下列说法正确的是( )| A. | 物体通过各点的瞬时速度之比为vB:vC:vD:vE=1:$\sqrt{2}$:$\sqrt{3}$:2 | |
| B. | 物体通过每一部分时,其速度增量vB-vA=vC-vB=vD-vC=vE-vD | |
| C. | 下滑全程的平均速度$\overline{v}$=vB | |
| D. | 物体由A点到各点所经历的时间之比为tB:tC:tD:tE=1:$\sqrt{2}$:$\sqrt{3}$:4 |