题目内容
2. 如图所示,电源的电动势E=8V,内阻r=5Ω,电路中电阻R2=5Ω,R1为滑动变阻器,其最大阻值为8Ω.
如图所示,电源的电动势E=8V,内阻r=5Ω,电路中电阻R2=5Ω,R1为滑动变阻器,其最大阻值为8Ω.(1)要使电源的输出功率最大,R1应取多大阻值?此时输出功率多大?R1、R2上的功率各多大?电源的效率多大?
(2)要使滑动变阻器上获得最大电功率,R1应是多大?此时R1消耗的功率为多大?
分析 (1)当外阻等于内阻时功率最大,由此明确滑动变阻器的接入电阻,再由闭合电路欧姆定律求得电流,最后求出各电阻消耗的功率以及电源的效率;
(2)当R1的电阻值等于内电阻和R2的电阻的和时,R1上的功率最大,求出此时的滑动变阻器阻值,再由闭合电路欧姆定律示得电流,即可求得此时功率.
解答 解:(1)因内阻为5Ω,当外阻等于内阻时功率最大,则即外阻为R外=5Ω=R2;所以此时滑动变阻器阻值为0;
此时电源的输出功率为:Pmax=I2R2=${(\frac{E}{{R}_{2}+r})}^{2}{R}_{2}$=($\frac{8}{5+5}$)2×5=3.2W;
此时滑动变阻器阻值为0,所以消耗的功率为0,而R2消耗的功率等于电源的输出功率,即3.2W
此时电源消耗的电功率:${P}_{总}=EI=\frac{{E}^{2}}{{R}_{2}+r}=\frac{{8}^{2}}{5+5}=6.4$W
电源的效率:η=$\frac{{P}_{max}}{{P}_{总}}$×100%=$\frac{3.2}{6.4}$×100%=50%
(2)同理,要使滑动变阻器上获得最大电功率,R1应等于电源的内阻与R2的和;由于R1的电阻小于电源的内阻与R2的和,可知R1的电阻值越大,消耗的电功率越大,即R1=8Ω时滑动变阻器上获得最大电功率.此时:
${P}_{R1}=(\frac{E}{{R}_{1}+{R}_{2}+r})^{2}•{R}_{1}$=$(\frac{8}{8+5+5})^{2}×8$=1.58W
答:(1)要使电源的输出功率最大,R1应取阻值为0;此时输出功率是3.2W;R1上的电功率是0,R2上的功率是3.2W;电源的效率是50%;
(2)要使滑动变阻器上获得最大电功率,R1应是取8Ω;此时R1消耗的功率为1.58W.
点评 本题考查闭合电路欧姆定律及功率公式,要注意电源最大输出功率的表达式及其结论的应用.

 学练快车道快乐假期暑假作业新疆人民出版社系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案 浙大优学小学年级衔接导与练浙江大学出版社系列答案
浙大优学小学年级衔接导与练浙江大学出版社系列答案 小学暑假作业东南大学出版社系列答案
小学暑假作业东南大学出版社系列答案 津桥教育暑假拔高衔接广东人民出版社系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案
| A. | 物体B受到5个力的作用 | |
| B. | 物体A向右运动的加速度为1m/s2 | |
| C. | 物体B受到地面的摩擦力是13.5N | |
| D. | 物体B受到地面的摩擦力是静摩擦力,若外力F增大到一定程度,则物体B可以运动 |
 功率可调的直流电动机线圈内阻恒为2Ω,接在电路中的A、B间,如图,电源的电动势为6V,内阻为2Ω,下列说法正确的是( )
功率可调的直流电动机线圈内阻恒为2Ω,接在电路中的A、B间,如图,电源的电动势为6V,内阻为2Ω,下列说法正确的是( )| A. | 电动机输出最大功率为2.25W | |
| B. | 电源的最大输出功率为4.5W | |
| C. | 电动机输出最大功率时电源输出功率也最大 | |
| D. | 若将电动机改为范围足够大的滑动变阻器,电源可输出得最大功率为4.5W |
 如图所示,内壁及碗口光滑的半球形碗固定在水平面上,碗口保持水平,A球、C球与B球分别用两根轻质细线连接,当系统保持静止时,B球对碗壁刚好无压力,图中θ=30°,则A球、C球的质量之比为( )
如图所示,内壁及碗口光滑的半球形碗固定在水平面上,碗口保持水平,A球、C球与B球分别用两根轻质细线连接,当系统保持静止时,B球对碗壁刚好无压力,图中θ=30°,则A球、C球的质量之比为( )| A. | 1:$\sqrt{3}$ | B. | $\sqrt{3}$:1 | C. | 1:2 | D. | 2:1 |
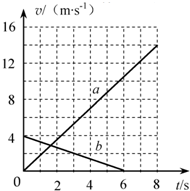 在平直公路上有A、B两辆汽车,质量均为6.0×103kg,运动时所受阻力均为车重的$\frac{1}{15}$.它们的v-t图象分别如图中a、b所示.求:
在平直公路上有A、B两辆汽车,质量均为6.0×103kg,运动时所受阻力均为车重的$\frac{1}{15}$.它们的v-t图象分别如图中a、b所示.求:
 一个半径较大的光滑球上端用绳子系在天花板上,下面和斜面接触,当斜面被水平向左移动时,悬绳中的拉力大小如何变化?
一个半径较大的光滑球上端用绳子系在天花板上,下面和斜面接触,当斜面被水平向左移动时,悬绳中的拉力大小如何变化?