题目内容
3. 如图所示,在某一水平面上有一轨道AC,其中AB段光滑,BC段粗糙,BC段与滑块之间的动摩擦因数为μ=0.2,有一质量为m=2kg的滑块从A点出发,以初速度v0=4m/s向右运动,恰能到达BC的中点,若滑块以初速度v0=4m/s从A点滑出的同时,给物体施加一水平向右、大小为1N的力F,则物体刚好能到达C,求:
如图所示,在某一水平面上有一轨道AC,其中AB段光滑,BC段粗糙,BC段与滑块之间的动摩擦因数为μ=0.2,有一质量为m=2kg的滑块从A点出发,以初速度v0=4m/s向右运动,恰能到达BC的中点,若滑块以初速度v0=4m/s从A点滑出的同时,给物体施加一水平向右、大小为1N的力F,则物体刚好能到达C,求:(1)B到C的距离.
(2)有力作用时,滑块从A运动到B点时的速度.
(3)A到B的距离.
分析 (1)物体在粗糙的水平面上运动的过程中,摩擦力做功,由动能定理即可求出B到BC的中点的距离,乘以2即为所求;
(2)B到C运动的过程中,摩擦力做功,由动能定理即可物体到达B点时的速度;
(3)A到B的过程中,拉力做功,由动能定理即可求出AB之间的距离.
解答 解:(1)物体从B滑到BC的中点的过程中,摩擦力做功,得:
$-μmg•\frac{L}{2}=0-\frac{1}{2}m{v}_{0}^{2}$
得:L=$\frac{{v}_{0}^{2}}{μg}=\frac{{4}^{2}}{0.2×10}m=8$m
(2)B到C运动的过程中,摩擦力做功,由动能定理得:$-μmgL=0-\frac{1}{2}m{v}_{B}^{2}$;
得:${v}_{B}=4\sqrt{2}$m/s
(3)A到B的过程中,拉力做功,由动能定理得:
$Fs=\frac{1}{2}m{v}_{B}^{2}-\frac{1}{2}m{v}_{0}^{2}$
所以:s=16m
答:(1)B到C的距离是8m.
(2)有力作用时,滑块从A运动到B点时的速度是$4\sqrt{2}$m/s.
(3)A到B的距离是16m.
点评 该题已知物体的受力求物体的运动,可以使用牛顿运动定律求解,由于没有时间,使用动能定理来求解更简单,便捷.

练习册系列答案
相关题目
11.在水底同一深度处并排放置着红、绿、紫、三只球,人在水面正上方竖在俯视,感觉最浅的球是( )
| A. | 红色球 | B. | 绿色球 | C. | 紫色球 | D. | 一样深浅 |
18.关于地球同步卫星下列说法正确的是( )
| A. | 地球同步卫星和地球同步,因此同步卫星的高度和线速度大小是一定的 | |
| B. | 地球同步卫星的角速度虽被确定,但高度和速度可以选择,高度增加,速度增大 | |
| C. | 地球同步卫星只能定点在赤道上空,相对地面静止不动 | |
| D. | 以上均不正确 |
8. 电动势为E、内阻为r的电源与定值电阻R1、R2及滑动变阻器R连接成如图所示的电路,当滑动变阻器的触头由中点滑向b端时,下列说法正确的是( )
电动势为E、内阻为r的电源与定值电阻R1、R2及滑动变阻器R连接成如图所示的电路,当滑动变阻器的触头由中点滑向b端时,下列说法正确的是( )
 电动势为E、内阻为r的电源与定值电阻R1、R2及滑动变阻器R连接成如图所示的电路,当滑动变阻器的触头由中点滑向b端时,下列说法正确的是( )
电动势为E、内阻为r的电源与定值电阻R1、R2及滑动变阻器R连接成如图所示的电路,当滑动变阻器的触头由中点滑向b端时,下列说法正确的是( )| A. | 电压表和电流表读数都减小 | B. | 电压表读数增大,电流表读数减小 | ||
| C. | 电压表读数减小,电流表读数增大 | D. | 电压表和电流表读数都增大 |
13. 在印度尼西亚的坤甸有一座著名的建筑,它正好建在赤道上,若某人造地球卫星在赤道上空飞行,卫星的轨道平面与地球赤道重合,已知卫星轨道半径为r,飞行方向与地球的自转方向相同,地球的自转角速度为ω0,地球半径为R,地球表面重力加速度为g,卫星在某时刻通过这一建筑物的正上方,则该卫星再次经过这个位置需要的最短时间为( )
在印度尼西亚的坤甸有一座著名的建筑,它正好建在赤道上,若某人造地球卫星在赤道上空飞行,卫星的轨道平面与地球赤道重合,已知卫星轨道半径为r,飞行方向与地球的自转方向相同,地球的自转角速度为ω0,地球半径为R,地球表面重力加速度为g,卫星在某时刻通过这一建筑物的正上方,则该卫星再次经过这个位置需要的最短时间为( )
 在印度尼西亚的坤甸有一座著名的建筑,它正好建在赤道上,若某人造地球卫星在赤道上空飞行,卫星的轨道平面与地球赤道重合,已知卫星轨道半径为r,飞行方向与地球的自转方向相同,地球的自转角速度为ω0,地球半径为R,地球表面重力加速度为g,卫星在某时刻通过这一建筑物的正上方,则该卫星再次经过这个位置需要的最短时间为( )
在印度尼西亚的坤甸有一座著名的建筑,它正好建在赤道上,若某人造地球卫星在赤道上空飞行,卫星的轨道平面与地球赤道重合,已知卫星轨道半径为r,飞行方向与地球的自转方向相同,地球的自转角速度为ω0,地球半径为R,地球表面重力加速度为g,卫星在某时刻通过这一建筑物的正上方,则该卫星再次经过这个位置需要的最短时间为( )| A. | $\frac{2π}{\sqrt{\frac{g{R}^{2}}{{r}^{3}}}}$ | B. | $\frac{2π}{{ω}_{0}+\sqrt{\frac{g{R}^{2}}{{r}^{3}}}}$ | C. | $\frac{2π}{{ω}_{0}-\sqrt{\frac{g{R}^{2}}{{r}^{3}}}}$ | D. | $\frac{2π}{\sqrt{\frac{g{R}^{2}}{{r}^{3}}}-{ω}_{0}}$ |
 如图,ABCD为一竖直平面的轨道,其中BC水平,长L=1米,A点比BC高出H=10米,AB和CD段轨道光滑.一质量为m=1千克的物体,从A点以v0=2米/秒的速度开始运动,经过BC后滑到高出C点h=9.8m的D点时速度为零.g取10m/s2,求:
如图,ABCD为一竖直平面的轨道,其中BC水平,长L=1米,A点比BC高出H=10米,AB和CD段轨道光滑.一质量为m=1千克的物体,从A点以v0=2米/秒的速度开始运动,经过BC后滑到高出C点h=9.8m的D点时速度为零.g取10m/s2,求: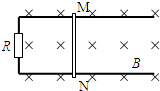 如图所示,宽度为L的足够长的平行金属导轨固定在绝缘水平面上,导轨的两端连接阻值R的电阻.导轨所在空间存在竖直向下的匀强磁场,磁感应强度为B,一根质量m的导体棒MN放在导轨上与导轨接触良好,导体棒的有效电阻也为R,导体棒与导轨间的动摩擦因数为μ,设最大静摩擦力等于滑动摩擦力.导体棒MN的初始位置与导轨最左端距离为L,导轨的电阻可忽略不计.
如图所示,宽度为L的足够长的平行金属导轨固定在绝缘水平面上,导轨的两端连接阻值R的电阻.导轨所在空间存在竖直向下的匀强磁场,磁感应强度为B,一根质量m的导体棒MN放在导轨上与导轨接触良好,导体棒的有效电阻也为R,导体棒与导轨间的动摩擦因数为μ,设最大静摩擦力等于滑动摩擦力.导体棒MN的初始位置与导轨最左端距离为L,导轨的电阻可忽略不计. 长为1.0m的长木板B静止放在水平冰面上,小物块A以某一初速度从木板B的左端滑上长木板B,直到A、B的速度达到相同,此时A、B的速度为0.4m/s,然后A、B又一起在水平冰面上滑行了16.0cm后停下.若小物块A可视为质点,它与长木板B的质量相同都为2kg,A、B间的动摩擦因数μ1=0.20.求:(取g=10m/s2)
长为1.0m的长木板B静止放在水平冰面上,小物块A以某一初速度从木板B的左端滑上长木板B,直到A、B的速度达到相同,此时A、B的速度为0.4m/s,然后A、B又一起在水平冰面上滑行了16.0cm后停下.若小物块A可视为质点,它与长木板B的质量相同都为2kg,A、B间的动摩擦因数μ1=0.20.求:(取g=10m/s2)