题目内容
20. 如图所示,竖直光滑半圆细管的半径r=0.4m,与水平光滑轨道AB在B点平滑连接,半径OC与竖直半径OB的夹角为60°,质量m=0.1kg小球(球的直径略小于细管半径),被弹簧枪水平发射后,沿水平轨道向左滑行,到达C点时速度vC=4m/s通过最高点后落于水平地面上,g取10m/s2.求:
如图所示,竖直光滑半圆细管的半径r=0.4m,与水平光滑轨道AB在B点平滑连接,半径OC与竖直半径OB的夹角为60°,质量m=0.1kg小球(球的直径略小于细管半径),被弹簧枪水平发射后,沿水平轨道向左滑行,到达C点时速度vC=4m/s通过最高点后落于水平地面上,g取10m/s2.求:(1)弹簧枪发射小物体前,弹簧的弹性势能;
(2)小球落地点到B点的距离;
(3)弹簧枪每次释放的弹性势能相同,调节半圆细管的半径,当细管半径等于多少时,小球落地点到B点的距离最大并计算最大值.
分析 (1)对运动到C的过程应用动能定理求解;
(2)对C到最高点运动过程应用机械能守恒求得在最高点的速度,然后根据平抛运动规律求得水平距离;
(3)对运动到最高点的过程应用动能定理求得在最高点的表达式,然后由平抛运动规律求得水平位移表达式,进而求得最大值.
解答 解:(1)小球在运动过程只有重力、弹簧弹力做功,故对小球运动到C的过程应用动能定理可得:${E}_{p}-mgr(1-cosθ)=\frac{1}{2}m{{v}_{C}}^{2}-0$;
所以,弹簧枪发射小物体前,弹簧的弹性势能${E}_{p}=mgr(1-cosθ)+\frac{1}{2}m{{v}_{C}}^{2}=1J$;
(2)小球从C到最高点的过程作用重力做功,机械能守恒,故有:$\frac{1}{2}m{{v}_{C}}^{2}=mgr(1+cosθ)+\frac{1}{2}m{v}^{2}$,所以,小球在最高点的速度$v=\sqrt{{{v}_{C}}^{2}-2gr(1+cosθ)}=2m/s$;
小球从最高点做平抛运动到水平地面上,故有$2r=\frac{1}{2}g{t}^{2}$,小球落地点到B点的距离$x=vt=2v\sqrt{\frac{r}{g}}=0.8m$;
(3)小球从静止到最高点的运动过程作用重力、支持力做功,由动能定理可得:${E}_{p}-2mgr′=\frac{1}{2}mv{′}^{2}$;
小球从最高点做平抛运动落到水平地面上,故有:$2r′=\frac{1}{2}g{t′}^{2}$,
小球落地点到B点的距离$x′=v′t′=\sqrt{\frac{2{E}_{p}}{m}-4gr′}•\sqrt{\frac{4r′}{g}}$=$2\sqrt{\frac{2}{gm}({E}_{p}r′-2mgr{′}^{2})}$=$2\sqrt{\frac{2}{mg}[-(\sqrt{2mg}r′-\frac{{E}_{p}}{2\sqrt{2mg}})^{2}+\frac{{{E}_{p}}^{2}}{8mg}]}$;
所以,当细管半径$r′=\frac{{E}_{p}}{4mg}$=$\frac{1}{4}m$时,小球落地点到B点的距离最大,最大值$x{′}_{max}=\frac{{E}_{p}}{mg}$=1m;
答:(1)弹簧枪发射小物体前,弹簧的弹性势能为1J;
(2)小球落地点到B点的距离为0.8m;
(3)弹簧枪每次释放的弹性势能相同,调节半圆细管的半径,当细管半径等于$\frac{1}{4}m$时,小球落地点到B点的距离最大且最大值为1m.
点评 经典力学问题一般先对物体进行受力分析,求得合外力及运动过程做功情况,然后根据牛顿定律、动能定理及几何关系求解.

 阅读快车系列答案
阅读快车系列答案| A. | 发射的子弹经0.5s击中目标 | |
| B. | 火车到站时间为17点30分 | |
| C. | 中央电视台新闻联播首播时间为19点整 | |
| D. | 2014年12月20日8点30分物理学科学业水平考试开考 |
| A. | 20J、5W | B. | 20J、10W | C. | 40J、10W | D. | 40J、20W |
 K在受到光照时能够发射光电子.阳极A吸收阴极K发出的光电子,在电路中形成光电流.如果用单色光a照射阴极K,电流表的指针发生偏转;用单色光b照射光电管阴极K时,电流表的指针不发生偏转.下列说法正确的是( )
K在受到光照时能够发射光电子.阳极A吸收阴极K发出的光电子,在电路中形成光电流.如果用单色光a照射阴极K,电流表的指针发生偏转;用单色光b照射光电管阴极K时,电流表的指针不发生偏转.下列说法正确的是( )| A. | a光的波长一定小于b光的波长 | |
| B. | 只增加a光的强度可能使通过电流表的电流增大 | |
| C. | 只增加a光的强度可使逸出的电子最大初动能变大 | |
| D. | 阴极材料的逸出功与入射光的频率有关 |
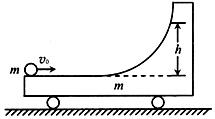 如图所示,质量为m的小车静置于光滑水平面上,小车右端带有光滑圆弧轨道,一质量也为m的小球以水平速度v0从左端冲上小车,到达某一高度h后又能回到小车左端,重力加速度为g,不计一切摩擦,以下说法正确的是( )
如图所示,质量为m的小车静置于光滑水平面上,小车右端带有光滑圆弧轨道,一质量也为m的小球以水平速度v0从左端冲上小车,到达某一高度h后又能回到小车左端,重力加速度为g,不计一切摩擦,以下说法正确的是( )| A. | 小球回到小车左端时速度为v0 | B. | 小球回到小车左端时速度为0 | ||
| C. | $h=\frac{v_0^2}{2g}$ | D. | $h=\frac{v_0^2}{4g}$ |
| A. |  | B. |  | C. |  | D. |  |
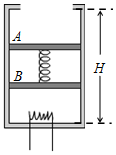 如图所示,导热气缸上端开口,竖直固定在地面上,高度H=1.05m.质量均为m=1kg的A、B两个活塞静止时将气缸容积均分为三等份,A、B之间为真空并压缩一根轻质弹簧,弹性系数k=400N/m,A、B与气缸间无摩擦.大气压P0=1×105Pa,密封气体初始温度T0=300K,重力加速度g取10m/s2,活塞面积S=2×10-3 m2,其厚度忽略不计.
如图所示,导热气缸上端开口,竖直固定在地面上,高度H=1.05m.质量均为m=1kg的A、B两个活塞静止时将气缸容积均分为三等份,A、B之间为真空并压缩一根轻质弹簧,弹性系数k=400N/m,A、B与气缸间无摩擦.大气压P0=1×105Pa,密封气体初始温度T0=300K,重力加速度g取10m/s2,活塞面积S=2×10-3 m2,其厚度忽略不计. 2016年9月15日,“天宫二号”空间实验室在酒泉卫星发射中心发射成功.“天宫二号”是中国第一个真正意义上的空间实验室.在“天宫二号”除了要验证航天员在轨中期驻留,还将开展14项空间科学和应用实验.10月19日“神州十一号”飞船与在距地面高度为h的圆轨道上运行的“天宫二号”教会对接成功,航天员景海鹏、陈冬进入“天宫二号”.航天员此次在“天宫二号”中期驻留时间为t.
2016年9月15日,“天宫二号”空间实验室在酒泉卫星发射中心发射成功.“天宫二号”是中国第一个真正意义上的空间实验室.在“天宫二号”除了要验证航天员在轨中期驻留,还将开展14项空间科学和应用实验.10月19日“神州十一号”飞船与在距地面高度为h的圆轨道上运行的“天宫二号”教会对接成功,航天员景海鹏、陈冬进入“天宫二号”.航天员此次在“天宫二号”中期驻留时间为t. 如图所示,将质量m=1.0kg的小物块放在长L=3.0m的平板车左端,车的上表面粗糙,物块与车上表面间的动摩擦因数μ=0.6,光滑半圆形固定轨道与光滑水平轨道在同一竖直平面内,半圆形轨道的半径r=1.2m,直径MON竖直,车的上表面和轨道最低点高度相同,开始时车和物块一起以v0=10m/s的初速度在水平轨道上向右运动,车碰到轨道后立即停止运动,取g=10m/s2,求:
如图所示,将质量m=1.0kg的小物块放在长L=3.0m的平板车左端,车的上表面粗糙,物块与车上表面间的动摩擦因数μ=0.6,光滑半圆形固定轨道与光滑水平轨道在同一竖直平面内,半圆形轨道的半径r=1.2m,直径MON竖直,车的上表面和轨道最低点高度相同,开始时车和物块一起以v0=10m/s的初速度在水平轨道上向右运动,车碰到轨道后立即停止运动,取g=10m/s2,求: