题目内容
12. 小车静止在光滑水平面上,站在车上的人练习打靶,靶装在车上的另一端,如图所示.已知车、人、枪和靶的总质量为M(不含子弹),每颗子弹质量为m,共n发,打靶时,枪口到靶的距离为d,若每发子弹打入靶中,就留在靶里,且待前一发打入靶中后,再打下一发.则以下说法正确的是( )
小车静止在光滑水平面上,站在车上的人练习打靶,靶装在车上的另一端,如图所示.已知车、人、枪和靶的总质量为M(不含子弹),每颗子弹质量为m,共n发,打靶时,枪口到靶的距离为d,若每发子弹打入靶中,就留在靶里,且待前一发打入靶中后,再打下一发.则以下说法正确的是( )| A. | 第n发子弹打入靶中后,小车应停在原来位置的右方 | |
| B. | 待打完n发子弹后,小车将以一定速度一直向右匀速运动 | |
| C. | 在每一发子弹的射击过程中,小车所发生的位移相同,大小均为$\frac{md}{nm+M}$ | |
| D. | 在每一发子弹的射击过程中,小车所发生的位移不相同,应越来越大 |
分析 子弹、枪、人、车组成的系统所受的合外力为零,系统的动量守恒;设子弹出口速度为v,根据动量守恒定律求解出车后退速度,计算出子弹飞到靶需要的时间和后退位移即可.
解答 解:AB、子弹、枪、人、车系统所受的合外力为零,系统的动量守恒.子弹射击前系统的总动量为零,子弹射入靶后总动量也为零,故小车仍然是静止的.在子弹射出枪口到打入靶中的过程中,小车向右运动,所以第n发子弹打入靶中后,小车应停在原来位置的右方.待打完n发子弹后,小车将静止不动,故A正确,B错误.
CD、设子弹出口速度为v,车后退速度大小为v′,以向左为正,根据动量守恒定律,有:
0=mv-[M+(n-1)m]v′…①
子弹匀速前进的同时,车匀速后退,故有:
vt+v′t=d…②
联立解得:v′=$\frac{mv}{M+(n-1)m}$,t=$\frac{d[M+(n-1)m]}{M+nm}$
故车后退位移大小为:△S=v′t=$\frac{md}{nm+M}$;
每颗子弹从发射到击中靶过程,小车均后退△S,故C正确,D错误;
故选:AC
点评 本题的关键是根据动量守恒定律求解出从发射一颗子弹到击中靶过程小车后退的距离,要找到子弹与小车位移关系.

练习册系列答案
相关题目
5.关于物理学的研究方法,下列叙述正确的是( )
| A. | 在不需要考虑物体本身的大小和形状时,用质点来代替物体的方法叫微元法 | |
| B. | 探究求合力的方法实验中采用了等效替代的方法 | |
| C. | 伽利略研究自由落体运动时,是将实验和逻辑推理结合起来的物理学研究方法 | |
| D. | 在推导匀变速直线运动的位移公式时,把整个运动过程划分成很多小段,每一段近似看作匀速直线运动,再把各段位移相加,这里运用了理想模型法 |
3.如图所示,固定在同一水平面上的两平行金属导轨AB、CD,两端接有阻值相同的两个定值电阻.质量为m的导体棒垂直放在导轨上,轻弹簧左端固定,右端连接导体棒,整个装置处于竖直向下的匀强磁场中.当导体棒静止在OO′位置时,弹簧处于原长状态.此时给导体棒一个水平向右的初速度v0,它能向右运动的最远距离为d,且能再次经过OO′位置.已知导体棒所受的摩擦力大小恒为f,导体棒向右运动过程中左侧电阻产生的热量为Q,不计导轨和导体棒的电阻.则( )
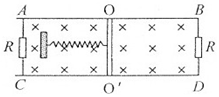

| A. | 弹簧的弹性势能最大为$\frac{1}{2}$mv02-Q-fd | |
| B. | 弹簧的弹性势能最大值大于$\frac{1}{2}$mv02-2Q-fd | |
| C. | 导体棒再次回到OO′位置时的动能等于$\frac{1}{2}$mv02-4Q-2fd | |
| D. | 导体棒再次回到OO′位置时的动能大于$\frac{1}{2}$mv02-4Q-2fd |
7.一个从地面竖直上抛的小球,到达最高点前1s上升的高度是它上升的最大高度的$\frac{1}{4}$,不计空气阻力,g=10m/s2.则( )
| A. | 小球上升的最大高度是5m | B. | 小球上抛的初速度是15m/s | ||
| C. | 2.5s时物体正在上升 | D. | 1s末、3s末物体处于同一位置 |
17.下列说法正确的是( )
| A. | 原子核式结构模型提出的实验基础是α粒子散射实验 | |
| B. | β 射线来自于原子核外电子的电离 | |
| C. | 目前秦山核电站主要利用重核裂变工作 | |
| D. | 光电效应实验中,光电子的最大初动能与入射光的频率成正比 |
4.下列各物理量属于标量的是( )
| A. | 线速度 | B. | 功 | C. | 动量 | D. | 冲量 |
13.如图所示,在同一水平面内有两根足够长的光滑水平金属导轨,间距为20$\sqrt{2}$ cm,电阻不计,其左端连接一阻值为10Ω的定值电阻,两导轨之间存在着磁感应强度为1T的匀强磁场,磁场边界虚线由多个正弦曲线的半周期衔接而成,磁场方向如图,一接入电阻阻值为10Ω的导体棒AB在外力作用下以10m/s的速度匀速向右运动,交流电压表和交流电流表均为理想电表,则( )
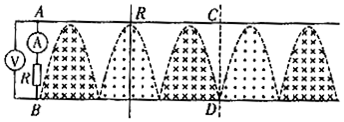

| A. | 电流表的示数是$\frac{\sqrt{2}}{10}$ A | |
| B. | 电压表的示数是1V | |
| C. | 导体棒运动到图示虚线CD位置时,电流表示数为零 | |
| D. | 导体棒上消耗的热功率为0.1W |
 如图所示,固定的竖直光滑U型金属导轨,间距为L,上端接有阻值为R的电阻,处在方向水平且垂直于导轨平面、磁感应强度为B的匀强磁场中.质量为m、电阻不计的导体棒与劲度系数为k的固定轻弹簧相连放在导轨上,导轨的电阻忽略不计.初始时刻,弹簧处于伸长状态,其伸长量为x1=$\frac{mg}{k}$,此时导体棒具有竖直向下的初速度v0.在沿导轨往复运动的过程中,导体棒始终与导轨垂直并保持良好接触.已知重力加速度为g.求:
如图所示,固定的竖直光滑U型金属导轨,间距为L,上端接有阻值为R的电阻,处在方向水平且垂直于导轨平面、磁感应强度为B的匀强磁场中.质量为m、电阻不计的导体棒与劲度系数为k的固定轻弹簧相连放在导轨上,导轨的电阻忽略不计.初始时刻,弹簧处于伸长状态,其伸长量为x1=$\frac{mg}{k}$,此时导体棒具有竖直向下的初速度v0.在沿导轨往复运动的过程中,导体棒始终与导轨垂直并保持良好接触.已知重力加速度为g.求: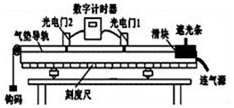 一同学想利用如图所示的气垫导轨实验装置探究动能定理.
一同学想利用如图所示的气垫导轨实验装置探究动能定理.