题目内容
9. 如图平行板电容器与电源相连,极板MN中间有小孔,极板MN的距离为d,质量为m,电量为+q的小球从距M板的A孔高h自由下落,小球落入电容器,N板的B孔开始返回.
如图平行板电容器与电源相连,极板MN中间有小孔,极板MN的距离为d,质量为m,电量为+q的小球从距M板的A孔高h自由下落,小球落入电容器,N板的B孔开始返回.(1)电容器相连的电源电压;
(2)若N板下移x,小球仍然从原处自由下落,小球穿过B孔的速度;
(3)若N板上移x,小球仍然从原处自由下落,小球距B孔距离为多少开始返回?
分析 (1)带电质点自A板上方相距为d的P点由静止自由下落(P、M、N在同一竖直线上),空气阻力不计,到达N孔时速度恰好为零,然后沿原路返回,根据动能定理即可求出;
(2)(3)在此过程中重力做功与电场力做功,移动上下极板,抓住两板间的电势差不变,通过动能定理判断带电质点的运动情况.
解答 解:(1)在极板间带电小球受重力和电场力,对整个过程,由动能定理有:
mg(h+d)-qU=0
可得:U=$\frac{mg(h+d)}{q}$
(2)在极板间带电小球受重力和电场力,对整个过程,由动能定理有:
mg(h+d+x)-qU=$\frac{1}{2}m{v}^{2}$
可得:v=$\sqrt{2gx}$
(3)若N板上移x,小球仍然从原处自由下落,当小球的速度等于0时,小球距B孔距离为x′则:
mg(h+d-x)-qU•$\frac{(d-x)-x′}{d-x}$=0
整理得:$x′=\frac{(d-x)x}{h+d}$
答:(1)电容器相连的电源电压是$\frac{mg(h+d)}{q}$;
(2)若N板下移x,小球仍然从原处自由下落,小球穿过B孔的速度是$\sqrt{2gx}$;
(3)若N板上移x,小球仍然从原处自由下落,小球距B孔距离为$\frac{(d-x)x}{h+d}$开始返回.
点评 对于本题选择全过程为研究过程,运用动能定理进行求解比较方便,在运用动能定理时,抓住电势差不变,电场力做功不变,比较电场力做功与重力做功的关系进行分析.

练习册系列答案
相关题目
12.下列关于布朗运动的说法,正确的是( )
| A. | 布朗运动是液体分子的无规则运动 | |
| B. | 液体温度越高,悬浮粒子越大,布朗运动越剧烈 | |
| C. | 布朗运动是由于液体各个部分的温度不同而引起的 | |
| D. | 布朗运动是由液体分子从各个方向对悬浮粒子撞击作用的不平衡引起的 |
17. 如图所示,固定于水平面内的直角形光滑杆,OM与ON段均足够长,转角处为光滑的小圆弧.质量均为m的A、B两个有孔小球串在杆上,且被长为L的轻绳相连.忽略两球的大小,初态时,它们的位置如图中虚线所示,两球均静止,绳处于伸直状态,且与OM平行.现对B球施加沿ON方向的恒定拉力F,当B球运动$\frac{3}{5}$L,两球位置如图中实线所示,此时B球的速度大小为( )
如图所示,固定于水平面内的直角形光滑杆,OM与ON段均足够长,转角处为光滑的小圆弧.质量均为m的A、B两个有孔小球串在杆上,且被长为L的轻绳相连.忽略两球的大小,初态时,它们的位置如图中虚线所示,两球均静止,绳处于伸直状态,且与OM平行.现对B球施加沿ON方向的恒定拉力F,当B球运动$\frac{3}{5}$L,两球位置如图中实线所示,此时B球的速度大小为( )
 如图所示,固定于水平面内的直角形光滑杆,OM与ON段均足够长,转角处为光滑的小圆弧.质量均为m的A、B两个有孔小球串在杆上,且被长为L的轻绳相连.忽略两球的大小,初态时,它们的位置如图中虚线所示,两球均静止,绳处于伸直状态,且与OM平行.现对B球施加沿ON方向的恒定拉力F,当B球运动$\frac{3}{5}$L,两球位置如图中实线所示,此时B球的速度大小为( )
如图所示,固定于水平面内的直角形光滑杆,OM与ON段均足够长,转角处为光滑的小圆弧.质量均为m的A、B两个有孔小球串在杆上,且被长为L的轻绳相连.忽略两球的大小,初态时,它们的位置如图中虚线所示,两球均静止,绳处于伸直状态,且与OM平行.现对B球施加沿ON方向的恒定拉力F,当B球运动$\frac{3}{5}$L,两球位置如图中实线所示,此时B球的速度大小为( )| A. | $\sqrt{\frac{32FL}{25m}}$ | B. | $\sqrt{\frac{96FL}{25m}}$ | C. | $\sqrt{\frac{96FL}{125m}}$ | D. | $\sqrt{\frac{32FL}{125m}}$ |
4.已知质量分别均匀的球壳对其内部物体的引力为零.科学家设想在赤道正上方高d处和正下方深为d处各修建一环形轨道,轨道面与赤道面共面.现有A、B两物体分别在上述两轨道中做匀速圆周运动,若地球半径为R,轨道对它们均无作用力,则两物体运动的向心加速度大小、线速度大小、角速度、周期之比为( )
| A. | $\frac{{a}_{A}}{{a}_{B}}$=($\frac{R-d}{R+d}$)2 | B. | $\frac{{v}_{A}}{{v}_{B}}$=$\sqrt{\frac{R-d}{R+d}}$ | ||
| C. | $\frac{{ω}_{A}}{{ω}_{B}}$=$\sqrt{\frac{(R-d)^{3}}{(R+d)^{3}}}$ | D. | $\frac{{T}_{A}}{{T}_{B}}$=$\sqrt{\frac{(R+d)^{3}}{{R}^{3}}}$ |
19.下列物理量是矢量的是( )
| A. | 动能 | B. | 功 | C. | 电势能 | D. | 电场强度 |
 质量m=0.06kg的物体置于水平桌面上,在F=2N的水平拉力作用下前进了l1=0.6m,如图所示,此时F停止作用,物体与桌面间的动摩擦因数μ=0.2,求:
质量m=0.06kg的物体置于水平桌面上,在F=2N的水平拉力作用下前进了l1=0.6m,如图所示,此时F停止作用,物体与桌面间的动摩擦因数μ=0.2,求: 在“验证机械能守恒定律”的实验中,已知电磁打点计时器所用的电源的频率为50Hz,查得当地的重力加速度g=9.80m/s2,测得所用的重物质量为1.00kg.实验中得到一条点迹清晰的纸带(如图所示),把第一个点记为O,另选连续的四个点A、B、C、D作为测量的点,经测量知道A、B、C、D各点到O点的距离分别为62.70cm、70.00cm、77.70cm、85.78cm.
在“验证机械能守恒定律”的实验中,已知电磁打点计时器所用的电源的频率为50Hz,查得当地的重力加速度g=9.80m/s2,测得所用的重物质量为1.00kg.实验中得到一条点迹清晰的纸带(如图所示),把第一个点记为O,另选连续的四个点A、B、C、D作为测量的点,经测量知道A、B、C、D各点到O点的距离分别为62.70cm、70.00cm、77.70cm、85.78cm.
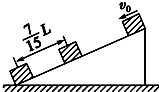 如图所示,小滑块在较长的斜面顶端,以初速度v0=2m/s、加速度a=2m/s2向下滑,在到达底端前1s内,所滑过的距离为斜面长度的$\frac{7}{15}$,求:小滑块在斜面上滑行的时间为多少?
如图所示,小滑块在较长的斜面顶端,以初速度v0=2m/s、加速度a=2m/s2向下滑,在到达底端前1s内,所滑过的距离为斜面长度的$\frac{7}{15}$,求:小滑块在斜面上滑行的时间为多少?