题目内容
20. 质量m=0.06kg的物体置于水平桌面上,在F=2N的水平拉力作用下前进了l1=0.6m,如图所示,此时F停止作用,物体与桌面间的动摩擦因数μ=0.2,求:
质量m=0.06kg的物体置于水平桌面上,在F=2N的水平拉力作用下前进了l1=0.6m,如图所示,此时F停止作用,物体与桌面间的动摩擦因数μ=0.2,求:(1)物体滑到l2=1.0m处时的速度;
(2)物体在桌面上滑行的总位移(g取10m/s2).
分析 (1)对物体滑到l2=1.0m处的过程中,运用动能定理列式即可求解速度;
(2)物体从运动到停止运动的整个过程,运用动能定理列式即可求解总位移.
解答 解:(1)由动能定理得:Fl1-μmgl2=$\frac{1}{2}m{v}^{2}$
解得:v=$\sqrt{\frac{2(F{l}_{1}-μmg{l}_{2})}{m}}=\sqrt{\frac{2×(2×0.6-0.2×0.06×10×1)}{0.06}}$=6m/s
(2)物体从运动到停止运动的整个过程,由动能定理得:
Fl1-μmgx=0-0
解得:x=$\frac{F{l}_{1}}{μmg}=\frac{2×0.6}{0.2×0.06×10}=10m$
答:(1)物体滑到l2=1.0m处时的速度为6m/s;
(2)物体在桌面上滑行的总位移为10m.
点评 本题主要考查了动能定理的直接应用,要求同学们能根据题目的需要,选择不同的过程运用动能定理求解,难度不大,属于基础题.

练习册系列答案
 同步练习河南大学出版社系列答案
同步练习河南大学出版社系列答案 同步练习西南大学出版社系列答案
同步练习西南大学出版社系列答案 补充习题江苏系列答案
补充习题江苏系列答案 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案
相关题目
3.氧气钢瓶充气后压强高于外界大气压,因某种原因,钢瓶缓慢漏气,假设缓慢漏气过程中瓶内外温度始终相等且保持不变,忽略氧气分子之间的相互作用.在漏气过程中,关于瓶内氧气的下列说法正确的是( )
| A. | 分子总数减少,分子总动能不变 | B. | 密度降低,分子平均动能不变 | ||
| C. | 吸收热量,对外做功 | D. | 压强降低,不对外做功 |
4.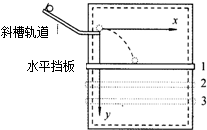 某物理实验小组采用如图所示的装置研究平抛运动.每次都将小球从斜槽的同一位置无初速释放,并从斜槽末端水平飞出.改变水平挡板的高度,就改变了小球在板上落点的位置,从而可描绘出小球的运动轨迹.某同学设想小球先后三次做平抛,将水平挡板依次放在1、2、3的位置,且l与2的间距等于2与3的间距.若三次实验中,小球从抛出点到落点的水平位移依次为xl、x2、x3,忽略空气阻力的影响,下面分析正确的是( )
某物理实验小组采用如图所示的装置研究平抛运动.每次都将小球从斜槽的同一位置无初速释放,并从斜槽末端水平飞出.改变水平挡板的高度,就改变了小球在板上落点的位置,从而可描绘出小球的运动轨迹.某同学设想小球先后三次做平抛,将水平挡板依次放在1、2、3的位置,且l与2的间距等于2与3的间距.若三次实验中,小球从抛出点到落点的水平位移依次为xl、x2、x3,忽略空气阻力的影响,下面分析正确的是( )
 某物理实验小组采用如图所示的装置研究平抛运动.每次都将小球从斜槽的同一位置无初速释放,并从斜槽末端水平飞出.改变水平挡板的高度,就改变了小球在板上落点的位置,从而可描绘出小球的运动轨迹.某同学设想小球先后三次做平抛,将水平挡板依次放在1、2、3的位置,且l与2的间距等于2与3的间距.若三次实验中,小球从抛出点到落点的水平位移依次为xl、x2、x3,忽略空气阻力的影响,下面分析正确的是( )
某物理实验小组采用如图所示的装置研究平抛运动.每次都将小球从斜槽的同一位置无初速释放,并从斜槽末端水平飞出.改变水平挡板的高度,就改变了小球在板上落点的位置,从而可描绘出小球的运动轨迹.某同学设想小球先后三次做平抛,将水平挡板依次放在1、2、3的位置,且l与2的间距等于2与3的间距.若三次实验中,小球从抛出点到落点的水平位移依次为xl、x2、x3,忽略空气阻力的影响,下面分析正确的是( )| A. | x2-xl=x3-x2 | B. | x2-xl<x3-x2 | C. | x2-xl>x3-x2 | D. | 无法判断 |
8. 如图所示,质量为m的物体A在竖直向上的力F(F<mg)作用下静止于斜面上.若减小力F,物体仍静止,则( )
如图所示,质量为m的物体A在竖直向上的力F(F<mg)作用下静止于斜面上.若减小力F,物体仍静止,则( )
 如图所示,质量为m的物体A在竖直向上的力F(F<mg)作用下静止于斜面上.若减小力F,物体仍静止,则( )
如图所示,质量为m的物体A在竖直向上的力F(F<mg)作用下静止于斜面上.若减小力F,物体仍静止,则( )| A. | 斜面对物体A的摩擦力不变 | B. | 斜面对物体A的支持力不变 | ||
| C. | 物体A所受合力不变 | D. | 斜面对物体A的摩擦力可能为零 |
15. 如图所示,位于竖直平面内的固定光滑圆环轨道与水平面相切于M点,与竖直墙相切于A点,竖直墙上另一点B与M的连线和水平面的夹角为60°,C是圆环上的一点,D是圆环轨道的圆心.已知在同一时刻释放4个小球:a、b、c两球分别由A、B、C三点从静止开始沿光滑倾斜直轨道运动到M点对应的时间分别是t1,t2,t3,d球由D点自由下落到M点的时间为t4,则( )
如图所示,位于竖直平面内的固定光滑圆环轨道与水平面相切于M点,与竖直墙相切于A点,竖直墙上另一点B与M的连线和水平面的夹角为60°,C是圆环上的一点,D是圆环轨道的圆心.已知在同一时刻释放4个小球:a、b、c两球分别由A、B、C三点从静止开始沿光滑倾斜直轨道运动到M点对应的时间分别是t1,t2,t3,d球由D点自由下落到M点的时间为t4,则( )
 如图所示,位于竖直平面内的固定光滑圆环轨道与水平面相切于M点,与竖直墙相切于A点,竖直墙上另一点B与M的连线和水平面的夹角为60°,C是圆环上的一点,D是圆环轨道的圆心.已知在同一时刻释放4个小球:a、b、c两球分别由A、B、C三点从静止开始沿光滑倾斜直轨道运动到M点对应的时间分别是t1,t2,t3,d球由D点自由下落到M点的时间为t4,则( )
如图所示,位于竖直平面内的固定光滑圆环轨道与水平面相切于M点,与竖直墙相切于A点,竖直墙上另一点B与M的连线和水平面的夹角为60°,C是圆环上的一点,D是圆环轨道的圆心.已知在同一时刻释放4个小球:a、b、c两球分别由A、B、C三点从静止开始沿光滑倾斜直轨道运动到M点对应的时间分别是t1,t2,t3,d球由D点自由下落到M点的时间为t4,则( )| A. | t1=t2=t3=t4 | B. | t4<t1=t3<t2 | C. | c球最先到达M点 | D. | t4<t3<t1<t2 |
5. 北斗卫星导航系统是中国自行研制的全球卫星导航系统.如图,两颗工作卫星1、2均绕地心做顺时针方向的匀速圆周运动,轨道半径为r,某时刻分别位于同一圆轨道上的A、B两位置.已知地球表面附近的重力加速度为g,地球半径为R.下列正确的是( )
北斗卫星导航系统是中国自行研制的全球卫星导航系统.如图,两颗工作卫星1、2均绕地心做顺时针方向的匀速圆周运动,轨道半径为r,某时刻分别位于同一圆轨道上的A、B两位置.已知地球表面附近的重力加速度为g,地球半径为R.下列正确的是( )
 北斗卫星导航系统是中国自行研制的全球卫星导航系统.如图,两颗工作卫星1、2均绕地心做顺时针方向的匀速圆周运动,轨道半径为r,某时刻分别位于同一圆轨道上的A、B两位置.已知地球表面附近的重力加速度为g,地球半径为R.下列正确的是( )
北斗卫星导航系统是中国自行研制的全球卫星导航系统.如图,两颗工作卫星1、2均绕地心做顺时针方向的匀速圆周运动,轨道半径为r,某时刻分别位于同一圆轨道上的A、B两位置.已知地球表面附近的重力加速度为g,地球半径为R.下列正确的是( )| A. | 卫星1加速也不可能追上卫星2 | |
| B. | 卫星1由位置A运动到位置B所需时间为$\frac{π}{3}\sqrt{\frac{r^3}{{g{R^2}}}}$ | |
| C. | 卫星1、2的万有引力一定相等 | |
| D. | 卫星1由位置A运动到位置B的过程中万有引力做正功 |
 如图所示,竖直放置的平行带电导体板A、B和水平放置的平行带电导体板C、D,B板上有一小孔,从小孔射出的带电粒子刚好可从C、D板间左上角切入C、D板间电场,已知C、D板间距离为d,长为2d,UAB=UCD=U>0,在C、D板右侧存在有一个垂直向里的匀强磁场.质量为m,电量为q的带正电粒子由静止从A板释放,沿直线运动至B板小孔后贴近C板进入C、D板间,最后恰好从D板右边缘进入磁场中.带电粒子的重力不计.求:
如图所示,竖直放置的平行带电导体板A、B和水平放置的平行带电导体板C、D,B板上有一小孔,从小孔射出的带电粒子刚好可从C、D板间左上角切入C、D板间电场,已知C、D板间距离为d,长为2d,UAB=UCD=U>0,在C、D板右侧存在有一个垂直向里的匀强磁场.质量为m,电量为q的带正电粒子由静止从A板释放,沿直线运动至B板小孔后贴近C板进入C、D板间,最后恰好从D板右边缘进入磁场中.带电粒子的重力不计.求: 如图平行板电容器与电源相连,极板MN中间有小孔,极板MN的距离为d,质量为m,电量为+q的小球从距M板的A孔高h自由下落,小球落入电容器,N板的B孔开始返回.
如图平行板电容器与电源相连,极板MN中间有小孔,极板MN的距离为d,质量为m,电量为+q的小球从距M板的A孔高h自由下落,小球落入电容器,N板的B孔开始返回. 竖直放置的半径R=80cm的半圆形光滑轨道与水平轨道相连接,连接点为P.质量为m=50g的小球以一定的初速度由水平轨道向左运动,并沿圆轨道的内壁运动到最高点M,如果球A经过N点时速度vN=8m/s,经过M点时对轨道的压力为0.5N.重力加速度g取10m/s2.求:
竖直放置的半径R=80cm的半圆形光滑轨道与水平轨道相连接,连接点为P.质量为m=50g的小球以一定的初速度由水平轨道向左运动,并沿圆轨道的内壁运动到最高点M,如果球A经过N点时速度vN=8m/s,经过M点时对轨道的压力为0.5N.重力加速度g取10m/s2.求: