题目内容
4.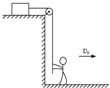 如图,质量为m的物体静止在光滑的平台上,系在物体上的绳子跨过光滑的定滑轮,由地面上的人拉着匀速向右以速度v0走动.则绳子与竖直方向夹角由0°变成45°过程中,人做功为( )
如图,质量为m的物体静止在光滑的平台上,系在物体上的绳子跨过光滑的定滑轮,由地面上的人拉着匀速向右以速度v0走动.则绳子与竖直方向夹角由0°变成45°过程中,人做功为( )| A. | $\frac{1}{2}$mv02 | B. | $\frac{{\sqrt{2}}}{2}$mv02 | C. | $\frac{1}{4}$mv02 | D. | mv02 |
分析 对人运动的速度进行分解,分解为沿绳子方向和垂直于绳子方向,在沿绳子方向上的分速度等于物块的速度,再根据动能定理求出人对滑块所做的功.
解答  解:将人的速度分解为沿绳子方向和垂直于绳子方向,在沿绳子方向的分速度大小等于物体的速度大小,则有:
解:将人的速度分解为沿绳子方向和垂直于绳子方向,在沿绳子方向的分速度大小等于物体的速度大小,则有:
v物=v0cos45°
根据动能定理:W=$\frac{1}{2}{mv}_{物}^{2}=\frac{1}{4}{mv}_{0}^{2}$
故选:C
点评 解决本题的关键是知道物体的速度等于沿绳子方向的速度,以及能够灵活运用动能定理

练习册系列答案
 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案
相关题目
14.对人造地球卫星,可以判断( )
| A. | 因为v=$\sqrt{gR}$,所以环绕速度随R增大而增大 | |
| B. | 因为v=$\sqrt{\frac{GM}{R}}$,所以环绕速度随R增大而减小 | |
| C. | 因为F=$\frac{GMm}{R2}$,所以当R增大到原来的2倍时,卫星所需的向心力减为原来的$\frac{1}{4}$ | |
| D. | 因为F=$\frac{m{v}^{2}}{R}$,所以当R增大到原来的2倍时,卫星所需的向心力减为原来的$\frac{1}{2}$ |
12.在离地面一定高处,以相同的动能竖直向上、竖直向下、斜向上、斜向下抛出多个质量相同的小球,这些小球到达地面时,有( )
| A. | 相同的动能 | B. | 相同的速度 | ||
| C. | 该过程重力做功的平均功率相同 | D. | 相同的加速度 |
16. 如图甲所示,甲、乙两个小球可视为质点,甲球沿倾角为30°的光滑足够长斜面由静止开始下滑,乙球做自由落体运动,甲、乙两球的动能与路程的关系图象如图乙所示.下列说法正确的是( )
如图甲所示,甲、乙两个小球可视为质点,甲球沿倾角为30°的光滑足够长斜面由静止开始下滑,乙球做自由落体运动,甲、乙两球的动能与路程的关系图象如图乙所示.下列说法正确的是( )
 如图甲所示,甲、乙两个小球可视为质点,甲球沿倾角为30°的光滑足够长斜面由静止开始下滑,乙球做自由落体运动,甲、乙两球的动能与路程的关系图象如图乙所示.下列说法正确的是( )
如图甲所示,甲、乙两个小球可视为质点,甲球沿倾角为30°的光滑足够长斜面由静止开始下滑,乙球做自由落体运动,甲、乙两球的动能与路程的关系图象如图乙所示.下列说法正确的是( )| A. | 甲球机械能不守恒,乙球机械能守恒 | |
| B. | 甲、乙两球的质量之比为m甲:m乙=4:1 | |
| C. | 甲、乙两球的动能均为Ek0时,两球重力的瞬时功率之比为P甲:P乙=1:1 | |
| D. | 甲、乙两球的动能均为Ek0时,两球下降高度之比h甲:h乙=1:4 |
13. 如图所示,质量为m的汽车,沿半径为R的半圆形拱桥运动,当汽车通过拱桥最高点B时速度大小为v,则此时拱桥对汽车的支持力大小为( )
如图所示,质量为m的汽车,沿半径为R的半圆形拱桥运动,当汽车通过拱桥最高点B时速度大小为v,则此时拱桥对汽车的支持力大小为( )
 如图所示,质量为m的汽车,沿半径为R的半圆形拱桥运动,当汽车通过拱桥最高点B时速度大小为v,则此时拱桥对汽车的支持力大小为( )
如图所示,质量为m的汽车,沿半径为R的半圆形拱桥运动,当汽车通过拱桥最高点B时速度大小为v,则此时拱桥对汽车的支持力大小为( )| A. | mg+m$\frac{v^2}{R}$ | B. | mg-m$\frac{v^2}{R}$ | C. | mg | D. | m$\frac{v^2}{R}$ |
14.在“蹦极”运动中,人由高空跃下到最低点的过程中( )
| A. | 重力对人做正功 | |
| B. | 人的重力势能减小了 | |
| C. | “蹦极”绳对人做负功 | |
| D. | 这个过程中只发生了重力势能和弹性势能之间的相互转化 |
 如图所示是研究电磁感应现象实验所需的器材,用实线将带有铁芯的线圈A、电源、滑动变阻器和开关连接成原线圈回路,将小量程电流表和线圈B连接成副线圈回路.并列举出在实验中改变副线圈回路磁通量,使副线圈回路产生感应电流的三种方式:
如图所示是研究电磁感应现象实验所需的器材,用实线将带有铁芯的线圈A、电源、滑动变阻器和开关连接成原线圈回路,将小量程电流表和线圈B连接成副线圈回路.并列举出在实验中改变副线圈回路磁通量,使副线圈回路产生感应电流的三种方式: