题目内容
10. 如图所示,空间内有方向垂直纸面(竖直面)向里的有界匀强磁场区域Ⅰ、Ⅱ,磁感应强度大小未知.区域I内有竖直向上的匀强电场,区域Ⅱ内有水平向右的匀强电场,两区域内的电场强度大小相等.现有一质量m=1×10-2kg、电荷量q=1×10-2C的带正电滑块从区域I左侧边界N点以v0=4m/s的初速度沿光滑的水平面向右运动,进入区域Ⅰ后,滑块立即在区域I竖直平面内做匀速圆周运动,并落在与边界MN相距L=2m的A点,取重力加速度g=10m/s2.
如图所示,空间内有方向垂直纸面(竖直面)向里的有界匀强磁场区域Ⅰ、Ⅱ,磁感应强度大小未知.区域I内有竖直向上的匀强电场,区域Ⅱ内有水平向右的匀强电场,两区域内的电场强度大小相等.现有一质量m=1×10-2kg、电荷量q=1×10-2C的带正电滑块从区域I左侧边界N点以v0=4m/s的初速度沿光滑的水平面向右运动,进入区域Ⅰ后,滑块立即在区域I竖直平面内做匀速圆周运动,并落在与边界MN相距L=2m的A点,取重力加速度g=10m/s2.(1)求匀强电场的电场强度大小E和区域I中磁场的磁感应强度大小B1;
(2)若滑块在N点以v1=6$\sqrt{2}$m/s的初速度沿水平面向右运动,当滑块经过Ⅰ区进入区域Ⅱ后恰好能沿直线运动,求区域Ⅱ内磁场的磁感应强度大小B2及有界磁场区域I的宽度d.
分析 (1)小球进入复合场区域后,小球立即在竖直平面内做匀速圆周运动,说明重力与电场力的大小相等,方向相反;小球离开磁场后做平抛运动,将运动分解,即可求出下落的高度,然后结合几何关系由于洛伦兹力提供向心力的公式即可求出磁感应强度;
(2)小球进入区域Ⅱ后恰好能沿直线运动,说明小球受到的合外力为0,受力分析即可求出小球的速度的大小,结合动能定理即可求出有界磁场区域Ⅰ的宽度d及区域Ⅱ的磁感应强度B2的大小.
解答 解:(1)小球进入复合场区域后,小球立即在竖直平面内做匀速圆周运动,说明重力与电场力的大小相等,方向相反;即:
qE=mg
所以:E=$\frac{mg}{q}=\frac{0.01×10}{0.01}=10$N/C
由于小球做匀速圆周运动,所以小球在复合场中运动的轨迹是半个圆,小球离开磁场后做平抛运动,将运动分解,水平方向:L=v0t1
得:${t}_{1}=\frac{L}{{v}_{0}}=\frac{2}{4}s=0.5$s
小球下落的高度:$h=\frac{1}{2}g{t}_{1}^{2}=\frac{1}{2}×10×0.{5}^{2}m=1.25$m
小球在复合场中运动的轨迹是半个圆,结合几何关系可得:h=2r
所以:r=$\frac{1}{2}$h=0.625m
小球做匀速圆周运动,洛伦兹力恰好提供向心力,得:$q{v}_{0}B=\frac{m{v}_{0}^{2}}{r}$
所以:B=$\frac{m{v}_{0}}{qr}=\frac{0.01×4}{0.01×0.625}=6.4$T
(2)小球进入区域Ⅱ后恰好能沿直线运动,说明小球受到的合外力为0,此时小球受到重力、水平方向的电场力和洛伦兹力的作用,由于电场力的大小与重力的大小相等,所以洛伦兹力的方向一定与重力、电场力的合力的方向相反,大小相等,如图:
由左手定则可知,小球运动的方向与x轴成45°角,洛伦兹力的大小:f=$\sqrt{2}$mg=$\sqrt{2}$×0.01×10=0.1$\sqrt{2}$N
又:f=qv2B2
所以:${B}_{2}=\frac{f}{q{v}_{2}}=\frac{0.1\sqrt{2}}{0.01×6\sqrt{2}}=\frac{5}{3}$T
小球在区域Ⅰ中仍然做匀速圆周运动,运动的半径:$r′=\frac{m{v}_{2}}{q{B}_{1}}=\frac{0.01×6\sqrt{2}}{0.01×6.4}=\frac{3\sqrt{2}}{3.2}$
小球在磁场中的偏转角是45°,由几何关系可得:$\frac{d}{r′}=sin45°$
所以:d=$\frac{\sqrt{2}}{2}r′=\frac{\sqrt{2}}{2}×\frac{3\sqrt{2}}{3.2}=\frac{3}{3.2}$m=$\frac{15}{16}$m
答:(1)匀强电场的电场强度是10N/C,区域Ⅰ中磁感应强度B1的大小是6.4T;
(2)有界磁场区域Ⅰ的宽度是$\frac{15}{16}$m,区域Ⅱ的磁感应强度B2的大小是$\frac{5}{3}$T.
点评 本题考查带电粒子在复合场中的运动,要注意当粒子在复合场中做匀速 圆周运动时,粒子受到的电场力与重力平衡.

 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案
| A. | 指针随着线圈转动而摆动,并且线圈旋转一周,指针左右摆动一次 | |
| B. | 当线圈平面转到跟磁力线垂直的平面位置时,电流表的指针的偏转最大 | |
| C. | 当线圈平面转到跟磁力线平行的位置时,电流表的指针的偏转最大 | |
| D. | 在匀强磁场中匀速转动的线圈里产生感应电动势和感应电流是按正弦规律变化的 |
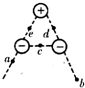 在真空中三个等量点电荷固定在正三角形的三个顶点,如图所示,c、d、e为三角形三个边的中点,下列判断正确的是( )
在真空中三个等量点电荷固定在正三角形的三个顶点,如图所示,c、d、e为三角形三个边的中点,下列判断正确的是( )| A. | d、e两点的电场强度相同 | |
| B. | d、e两点的电势相等 | |
| C. | 电子在a点的电势能高于在b点的电势能 | |
| D. | d点的场强大于c点的场强 |
| A. | 50 N | B. | 500 N | C. | 500$\sqrt{2}$ N | D. | 10 00 N |
 如图所示,A和B为两等量异号电荷,A带正电,B带负电.在A、B的连线上有a、b、c三点,其中b为连线的中点,a、c两点与b点等距,则( )
如图所示,A和B为两等量异号电荷,A带正电,B带负电.在A、B的连线上有a、b、c三点,其中b为连线的中点,a、c两点与b点等距,则( )| A. | a点与c点的电场强度相同 | |
| B. | a点与c点的电势相同 | |
| C. | a、b间的电势差与b、c间的电势差相同 | |
| D. | 过b点做A、B连线的垂线,点电荷q沿此垂线方向移动,电荷的电势能保持不变 |
 光滑的$\frac{1}{4}$圆弧轨道固定在竖直平面内,与水平轨道CE连接.水平轨道的CD段光滑、DE段粗糙.一根轻质弹簧一端固定在C处的竖直面上,弹簧处于自然长度.将质量为m的物块a从顶端F点静止释放后,沿圆弧轨道下滑.
光滑的$\frac{1}{4}$圆弧轨道固定在竖直平面内,与水平轨道CE连接.水平轨道的CD段光滑、DE段粗糙.一根轻质弹簧一端固定在C处的竖直面上,弹簧处于自然长度.将质量为m的物块a从顶端F点静止释放后,沿圆弧轨道下滑.



 如图,一个物体静止放在水平面上,在跟竖直方向成θ角为37度的斜向下的推力F=20N的作用下沿水平移动的距离s=5m,若物体的质量为m=0.4kg,物体与地面之间的动摩擦因数μ=0.2,(g=10m/s2,sin37.=0.6,cos37.=0.8)求:
如图,一个物体静止放在水平面上,在跟竖直方向成θ角为37度的斜向下的推力F=20N的作用下沿水平移动的距离s=5m,若物体的质量为m=0.4kg,物体与地面之间的动摩擦因数μ=0.2,(g=10m/s2,sin37.=0.6,cos37.=0.8)求: 如图所示,一质量M=20kg横截面积S=2×10-3m2的活塞封闭一定质量的理想气体,气缸壁导热良好,摩擦不计,当气体的温度由17℃缓慢增为27℃时活塞上升了1cm;现保持气体温度27℃不变,在活塞上面缓慢加上m=10kg的细沙,求此时活塞离气缸底部的高度.(取g=10m/s2,大气压强po=1.0×105pa)
如图所示,一质量M=20kg横截面积S=2×10-3m2的活塞封闭一定质量的理想气体,气缸壁导热良好,摩擦不计,当气体的温度由17℃缓慢增为27℃时活塞上升了1cm;现保持气体温度27℃不变,在活塞上面缓慢加上m=10kg的细沙,求此时活塞离气缸底部的高度.(取g=10m/s2,大气压强po=1.0×105pa)