题目内容
14. 特警在某次训练时场地如图所示:一根足够长的钢性轻绳竖直悬挂,其左侧有一高度差H=3m的滑道AB,右侧有一平台PQ.已知B、C、P三点等高,C点是轻绳上一点,BC距离x1=2.4m,MC的长度l=3.2m.训练时,一质量m=70kg的特警(可视为质点)从A点静止滑下,在B点以v=6m/s的速度水平飞出,接近轻绳时他迅速抓住绳子,因绳子不可伸长他沿绳子方向的速度立即为零,然后随轻绳摆至最高点时松手,落于平台PQ上g=10m/s2,空气阻力不计.
特警在某次训练时场地如图所示:一根足够长的钢性轻绳竖直悬挂,其左侧有一高度差H=3m的滑道AB,右侧有一平台PQ.已知B、C、P三点等高,C点是轻绳上一点,BC距离x1=2.4m,MC的长度l=3.2m.训练时,一质量m=70kg的特警(可视为质点)从A点静止滑下,在B点以v=6m/s的速度水平飞出,接近轻绳时他迅速抓住绳子,因绳子不可伸长他沿绳子方向的速度立即为零,然后随轻绳摆至最高点时松手,落于平台PQ上g=10m/s2,空气阻力不计.(1)特警在滑道AB上克服摩擦力做了多少功?
(2)特警在抓轻绳后的瞬间,绳子上的拉力T为多少?
(3)为了确保特警安全地落在平台上,平台最左侧的点P到轻绳的水平距离x2应处于怎样的范围?
分析 (1)在AB段由动能定理求的摩擦力做功
(2)从B点做平抛运动,根据平抛运动的特点求的下降的高度,根据牛顿第二定律求的拉力;
(3)从最低点到最高点有几何关系求的 p点距离
解答 解:(1)在AB段由动能定理可得$mgh-{W}_{f}=\frac{1}{2}m{v}^{2}-0$
解得Wf=840J
(2)从B点做平抛运动,在水平方向做匀速则t=$\frac{{x}_{1}}{v}=\frac{2.4}{6}s$=0.4s
竖直方向的速度为vy=gt=4m/s
下降的高度为h=$h=\frac{1}{2}g{t}^{2}=\frac{1}{2}×10×0.{4}^{2}m=0.8m$
抓住绳子瞬间的速度为v′=v=6m/s
在抓住绳子瞬间由T-mg=$\frac{m{v′}^{2}}{R}$
其中R=0.8+3.2m=4m
解得T=1330N
(3)从最低点到P点由动能定理可得$-mgh′=0-\frac{1}{2}mv{′}^{2}$解得h′=1.8m
有几何关系可知SP=$\sqrt{{R}^{2}-{l}^{2}}=2.4m$
OU=$\sqrt{{R}^{2}-(R-h′)^{2}}=3.2m$
故x2的取值范围为2.4m≤x2≤3.2
答:(1)特警在滑道AB上克服摩擦力做功为840J
(2)特警在抓轻绳后的瞬间,绳子上的拉力T为1330N
(3)为了确保特警安全地落在平台上,平台最左侧的点P到轻绳的水平距离x2应处2.4m≤x2≤3.2m
点评 本题运动过程复杂,分析清楚物体运动过程,应用动能定理,牛顿第二定律、几何关系即可正确解题

练习册系列答案
相关题目
13. 如图所示,长为L的轻绳一端固定在O点,另一端系一质量为m的小球,在最低点给小球一水平初速度v0,同时对小球施加一大小不变,方向始终垂直于绳的力F,小球沿圆周运动到绳水平时,小球速度大小恰好也为v0.则正确的是( )
如图所示,长为L的轻绳一端固定在O点,另一端系一质量为m的小球,在最低点给小球一水平初速度v0,同时对小球施加一大小不变,方向始终垂直于绳的力F,小球沿圆周运动到绳水平时,小球速度大小恰好也为v0.则正确的是( )
 如图所示,长为L的轻绳一端固定在O点,另一端系一质量为m的小球,在最低点给小球一水平初速度v0,同时对小球施加一大小不变,方向始终垂直于绳的力F,小球沿圆周运动到绳水平时,小球速度大小恰好也为v0.则正确的是( )
如图所示,长为L的轻绳一端固定在O点,另一端系一质量为m的小球,在最低点给小球一水平初速度v0,同时对小球施加一大小不变,方向始终垂直于绳的力F,小球沿圆周运动到绳水平时,小球速度大小恰好也为v0.则正确的是( )| A. | 小球在向上摆到45°角时速度达到最大 | |
| B. | F=mg | |
| C. | 速度大小始终不变 | |
| D. | F=$\frac{2mg}{π}$ |
2. 等腰直角三角形OPQ区域内存在匀强磁场.另有一等腰直角三角形导线框ABC以恒定的速度沿如图所示方向穿过磁场.关于线框中的感应电流,以下说法中正确的是( )
等腰直角三角形OPQ区域内存在匀强磁场.另有一等腰直角三角形导线框ABC以恒定的速度沿如图所示方向穿过磁场.关于线框中的感应电流,以下说法中正确的是( )
 等腰直角三角形OPQ区域内存在匀强磁场.另有一等腰直角三角形导线框ABC以恒定的速度沿如图所示方向穿过磁场.关于线框中的感应电流,以下说法中正确的是( )
等腰直角三角形OPQ区域内存在匀强磁场.另有一等腰直角三角形导线框ABC以恒定的速度沿如图所示方向穿过磁场.关于线框中的感应电流,以下说法中正确的是( )| A. | 开始进入磁场时感应电流沿顺时针方向 | |
| B. | 开始进入磁场时感应电流一定最大 | |
| C. | 开始穿出磁场时感应电流一定最大 | |
| D. | 即将穿出磁场时感应电流一定最小 |
6.如图所示为两电阻R1、R2的电流I和电压U的关系图线,由图可知,两电阻的大小之比R1:R2是( )


| A. | 1:3 | B. | 3:1 | C. | 1:$\sqrt{3}$ | D. | $\sqrt{3}$:1 |

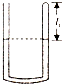 一端封闭的粗细均匀的U形管,用水银封闭一定质量的空气(可看成理想气体),当管内空气温度为t1=31℃时,U型管两边水银面等高,如图所示,此时空气柱长l1=8cm,(设大气压强恒为p0=76cmHg)求:
一端封闭的粗细均匀的U形管,用水银封闭一定质量的空气(可看成理想气体),当管内空气温度为t1=31℃时,U型管两边水银面等高,如图所示,此时空气柱长l1=8cm,(设大气压强恒为p0=76cmHg)求: