题目内容
4.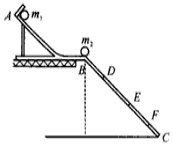 为了验证碰撞中的动量守恒和检验两个小球的碰撞是否为弹性碰撞(碰撞过程中没有机械能损失),某同学选取了两个体积相同、质量不等的小球,按下述步骤做如下实验:
为了验证碰撞中的动量守恒和检验两个小球的碰撞是否为弹性碰撞(碰撞过程中没有机械能损失),某同学选取了两个体积相同、质量不等的小球,按下述步骤做如下实验:①用天平测出两个小球的质量分别为m1和m2,且m1>m2;
②按照如图所示的那样,安装好实验装置.将斜槽AB固定在桌边,使槽的末端点的切线水平,将一斜面BC连接在斜槽末端;
③先不放小球m2,让小球m1从斜槽顶端A处由静止开始滚下,记下小球在斜面上的落点位置;
④将小球m2放在斜槽前端边缘处,让小球m1仍从斜槽顶端A处静止开始滚下,使它们发生碰撞,记下小球m1和小球m2在斜面上的落点位置;
⑤用毫米刻度尺量出各个落点位置到斜槽末端点B的距离.图中D、E、F点是该同学记下的小球在斜面上的几个落点位置,到B点的距离分别为LD、LE、LF
根据该同学的实验,回答下列问题:
(1)在没有放m2时,让小球m1从斜槽顶端A处由静止开始滚下,m1的落点是图中的E点;
(2)用测得的物理量来表示,只要满足关系式m1$\sqrt{{L}_{E}}$=m1$\sqrt{{L}_{D}}$+m2$\sqrt{{L}_{F}}$,则说明碰撞中动量是守的;
(3)用测得的物理量来表示,只要再满足关系式m1LE=m1LD+m2LF,则说明两小球的碰撞是弹性碰撞.
分析 (1)小球m1和小球m2相撞后,小球m2的速度增大,小球m1的速度减小,都做平抛运动,由平抛运动规律不难判断出;
(2)设斜面BC与水平面的倾角为α,由平抛运动规律求出碰撞前后小球m1和小球m2的速度,表示出动量的表达式即可求解;
(3)若两小球的碰撞是弹性碰撞,则碰撞前后机械能没有损失.
解答 解:(1)小球m1和小球m2相撞后比没有碰撞时m1的变小,碰撞后m1的水平位移变小,碰撞后m1的速度小于m2的速度,由图示可知,在没有放m2时,让小球m1从斜槽顶端A处由静止开始滚下,m1的落点是图中的E点,碰撞后m1球的落地点是D点,m2球的落地点是F点;
(2)碰撞前,小于m1落在图中的E点,设其水平初速度为v1.小球m1和m2发生碰撞后,m1的落点在图中的D点,设其水平初速度为v1′,m2的落点是图中的F点,设其水平初速度为v2. 设斜面BC与水平面的倾角为α,
由平抛运动规律得:LDsinα=$\frac{1}{2}$gt2,LDcosα=v1′t,解得:v1′=$\sqrt{\frac{g{L}_{D}(cosα)^{2}}{2sinα}}$,
同理可解得:v1=$\sqrt{\frac{g{L}_{E}(cosα)^{2}}{2sinα}}$,v2=$\sqrt{\frac{g{L}_{F}(cosα)^{2}}{2sinα}}$,
所以只要满足m1v1=m2v2+m1v1′,即:m1$\sqrt{\frac{g{L}_{E}(cosα)^{2}}{2sinα}}$=m2$\sqrt{\frac{g{L}_{F}(cosα)^{2}}{2sinα}}$+m1$\sqrt{\frac{g{L}_{D}(cosα)^{2}}{2sinα}}$,
m1$\sqrt{{L}_{E}}$=m1$\sqrt{{L}_{D}}$+m2$\sqrt{{L}_{F}}$,则说明两球碰撞过程中动量守恒;
(3)若两小球的碰撞是弹性碰撞,则碰撞前后机械能没有损失.
则要满足关系式:$\frac{1}{2}$m1v12=$\frac{1}{2}$m1v1′2+$\frac{1}{2}$m2v22,整理得:m1LE=m1LD+m2LF;
故答案为:(1)E;(2)m1$\sqrt{{L}_{E}}$=m1$\sqrt{{L}_{D}}$+m2$\sqrt{{L}_{F}}$;(3)m1LE=m1LD+m2LF.
点评 本题考查了验证碰撞中的动量守恒定律实验,知道分析清楚图示实验、理解实验原理是解题的关键,学会运用平抛运动的基本规律求解碰撞前后的速度,两小球的碰撞是弹性碰撞,则碰撞前后机械能没有损失.

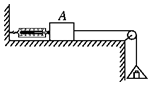 如图所示,放在水平桌面上的木块A处于静止状态,所挂的砝码和托盘的总质量为0.6kg,弹簧测力计读数为2N,滑轮摩擦不计.若轻轻取走盘中的部分砝码,使砝码和托盘的总质量减少到0.3kg,则将会出现的情况是(g取10m/s2)( )
如图所示,放在水平桌面上的木块A处于静止状态,所挂的砝码和托盘的总质量为0.6kg,弹簧测力计读数为2N,滑轮摩擦不计.若轻轻取走盘中的部分砝码,使砝码和托盘的总质量减少到0.3kg,则将会出现的情况是(g取10m/s2)( )| A. | 弹簧测力计的读数将不变 | B. | A仍静止不动 | ||
| C. | A与桌面间的摩擦力不变 | D. | A所受的合力将要变大 |
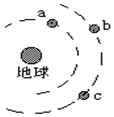 如图所示,a、b、c是地球大气层外圆形轨道上运动的三颗卫星,a和b质量相等且小于c的质量,则( )
如图所示,a、b、c是地球大气层外圆形轨道上运动的三颗卫星,a和b质量相等且小于c的质量,则( )| A. | b所需向心力最小 | |
| B. | b、c的周期相同且大于a的周期 | |
| C. | b、c的向心加速度大小相等,且大于a的向心加速度 | |
| D. | b、c的线速度大小相等,且大于a的线速度 |
| A. | 为实现对接,两者运行速度的大小都应介于第一宇宙速度和第二宇宙速度之间 | |
| B. | 航天员在天宫二号中处于失重状态,说明航天员不受地球引力作用 | |
| C. | 如不干涉,天宫二号的轨道高度将缓慢增加 | |
| D. | 如不加干预,在运行一段时间后,天宫二号的动能会增加 |
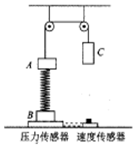 某同学利用图示装置来研究机械能守恒问题,设计了如下实验.
某同学利用图示装置来研究机械能守恒问题,设计了如下实验.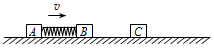 如图所示,质量均为m的两滑块A、B间压缩着一个弹性势能为mv2的轻弹簧,弹簧与A、B不栓接,滑块A、B用细线相连.A、B以相同的速度v沿光滑水平面匀速运动,能与质量也为m的静止滑块C发生正碰,且碰撞瞬间细线断裂,碰后B、C粘在一起.在以后的运动过程中.
如图所示,质量均为m的两滑块A、B间压缩着一个弹性势能为mv2的轻弹簧,弹簧与A、B不栓接,滑块A、B用细线相连.A、B以相同的速度v沿光滑水平面匀速运动,能与质量也为m的静止滑块C发生正碰,且碰撞瞬间细线断裂,碰后B、C粘在一起.在以后的运动过程中.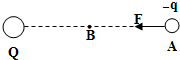 把一检验电荷q放在点电荷Q所形成的电场中的A点,若检验电荷的电量为q=-2.0×10-8C,它所受的电场力F=4.0×10-3N,方向指向Q,如图所示,A点到Q的距离为r=0.30m,已知静电常量K=9×109N•m2/C2,试求:
把一检验电荷q放在点电荷Q所形成的电场中的A点,若检验电荷的电量为q=-2.0×10-8C,它所受的电场力F=4.0×10-3N,方向指向Q,如图所示,A点到Q的距离为r=0.30m,已知静电常量K=9×109N•m2/C2,试求: