题目内容
5.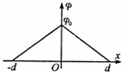 静电场方向平行于x轴,其电势φ随x的分布如图中折线所示,其中φ0和d已知.一个带负电的粒子在电场中以O为中心,沿x轴方向做周期性运动.已知该粒子质量为m、电荷量为-q,其动能与电势能之和为-A(0<A<qφ0).不计重力,下列说法正确的是( )
静电场方向平行于x轴,其电势φ随x的分布如图中折线所示,其中φ0和d已知.一个带负电的粒子在电场中以O为中心,沿x轴方向做周期性运动.已知该粒子质量为m、电荷量为-q,其动能与电势能之和为-A(0<A<qφ0).不计重力,下列说法正确的是( )| A. | Od间是匀强电场,电场强度大小为$\frac{φ_0}{2d}$ | |
| B. | 粒子运动过程中与O的最大距离为(1-$\frac{A}{qφ_0}$)d | |
| C. | 粒子的加速度大小为$\frac{qφ_0}{md}$ | |
| D. | 粒子完成一次往复运动的时间为$\frac{2d}{qφ_0}$$\sqrt{2m(qφ_0-A)}$ |
分析 由图可知Od间电势随x均匀变化,则可知电场为匀强电场,由电势差与电场强度的关系可求得电场强度;由题意可知,动能与电势能之和保持不变,设出运动区间为[-x,x],由题意可知x处的电势,则由数学关系可求得x值,得到粒子运动过程中与O的最大距离.粒子在区间内做周期性变化,且从最远点到O点时做匀变速直线运动,由运动学规律可求得粒子完成一次往复运动的时间.
解答 解:A、由图可知,0与d两点间的电势差为φ0,电场强度的大小为 E=$\frac{{φ}_{0}}{d}$,则知Od间是匀强电场,故A错误.
B、设粒子在[-x,x]区间内运动,速率为v,由题意得 $\frac{1}{2}$mv2-qφ=-A
由图可知 φ=φ0(1-$\frac{|x|}{d}$)
由①②得 $\frac{1}{2}$mv2=qφ0(1-$\frac{|x|}{d}$)-A
因动能非负,有 qφ0(1-$\frac{|x|}{d}$)-A≥0
得|x|≤(1-$\frac{A}{qφ_0}$)d.即粒子运动过程中与O的最大距离为(1-$\frac{A}{qφ_0}$)d.故B正确.
C、考虑粒子从-x0处开始运动的四分之一周期
根据牛顿第二定律,粒子的加速度 a=$\frac{F}{m}$=$\frac{qE}{m}$=$\frac{qφ_0}{md}$.故C正确.
D、粒子从-x0处开始运动的四分之一周期内做匀加速直线运动,用时 t=$\sqrt{\frac{2{x}_{0}}{a}}$
粒子完成一次往复运动的时间为 T=4t
解得 T=$\frac{4d}{q{φ}_{0}}$$\sqrt{2m(q{φ}_{0}-A)}$.故D错误.
故选:BC
点评 本题要明确图象的斜率表示电场强度,能从图象中判断出电场的性质,并能灵活应用功能关系结合数学知识和周期性研究.

 名师金手指领衔课时系列答案
名师金手指领衔课时系列答案| A. | 顾客受到重力和支持力的作用 | |
| B. | 顾客受到重力、支持力和摩擦力的作用 | |
| C. | 顾客受到的合外力方向保持水平 | |
| D. | 顾客受到的合外力方向保持竖直 |
 如图所示,半圆形凹槽的圆心为O点.在与O点等高的边缘A、B两点处分别以速度v1、v2水平同时相向抛出两个小球,两小球恰好落在弧面上的P点.已知∠AOP=60°,不计空气阻力.则以下说法中正确的是( )
如图所示,半圆形凹槽的圆心为O点.在与O点等高的边缘A、B两点处分别以速度v1、v2水平同时相向抛出两个小球,两小球恰好落在弧面上的P点.已知∠AOP=60°,不计空气阻力.则以下说法中正确的是( )| A. | v1:v2=1:2 | |
| B. | 若只增大v1,两小球可在空中相遇 | |
| C. | 若要使两小球落在P点右侧的弧面上同一点,则应同时增大v1、v2 | |
| D. | 若改变v1、v2的大小,只要两小球落在弧面上的同一点,则v1:和v2的大小之和就不变 |
| A. | 4.9 km/s | B. | 7.9 km/s | C. | 11.2 km/s | D. | 16.7 km/s |

| A. | 加速度逐渐减小 | B. | 粒子一定带正电 | ||
| C. | 电场力对粒子做正功 | D. | 粒子电势能增加,动能减少 |
 某物理学习小组中甲、乙两同学分别做了以下实验.
某物理学习小组中甲、乙两同学分别做了以下实验. 中国北京获得得2020年冬奥会举办权,跳台滑雪是冬季奥运会的比赛项目之一.如图,滑雪运动员从滑台A起跳,在助滑坡AB上取得较高速度后,在跳台的C点跳出,在着路坡CD的某点P着路.已知AB与BC圆滑相接,A离地的高度为H,C点离地高度为h,设质量为m的滑雪运动员从A点由静止滑下,离开C点时的速度为v,着落坡CD与水平面的夹角为θ,重力加速度为g,运动员可以看作质点,空气阻力不计,取地面为参考平面,求:
中国北京获得得2020年冬奥会举办权,跳台滑雪是冬季奥运会的比赛项目之一.如图,滑雪运动员从滑台A起跳,在助滑坡AB上取得较高速度后,在跳台的C点跳出,在着路坡CD的某点P着路.已知AB与BC圆滑相接,A离地的高度为H,C点离地高度为h,设质量为m的滑雪运动员从A点由静止滑下,离开C点时的速度为v,着落坡CD与水平面的夹角为θ,重力加速度为g,运动员可以看作质点,空气阻力不计,取地面为参考平面,求: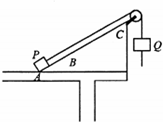 水平台面上固定一倾角为37°的斜面ABC,A为斜面的底端点,C为顶端点,AB部分光滑,长度sAB=1.0m;BC部分粗糙,长度sBC=2.0m.在斜面顶端C处固定一质量不计的光滑定滑轮,一根细绳绕过滑轮,左端系在A处质量m=1.0kg的滑块P(可视为质点)上,右侧竖直部分穿上质量M=1.0kg的物块Q.已知P与BC部分的动摩擦因数μ=0.7,当绳中张力超过9.6N时物块Q与绳间就会出现相对滑动,且绳与Q间的摩擦力恒为F=9.6N.开始时,P、Q均静止,绳处于伸直状态.现同时释放P和Q,已知在P上滑过程中Q不会从绳上滑脱也不会落地,取g=10m/s2,试分析:(sin37°=0.6)
水平台面上固定一倾角为37°的斜面ABC,A为斜面的底端点,C为顶端点,AB部分光滑,长度sAB=1.0m;BC部分粗糙,长度sBC=2.0m.在斜面顶端C处固定一质量不计的光滑定滑轮,一根细绳绕过滑轮,左端系在A处质量m=1.0kg的滑块P(可视为质点)上,右侧竖直部分穿上质量M=1.0kg的物块Q.已知P与BC部分的动摩擦因数μ=0.7,当绳中张力超过9.6N时物块Q与绳间就会出现相对滑动,且绳与Q间的摩擦力恒为F=9.6N.开始时,P、Q均静止,绳处于伸直状态.现同时释放P和Q,已知在P上滑过程中Q不会从绳上滑脱也不会落地,取g=10m/s2,试分析:(sin37°=0.6)