题目内容

11．一质量为m的物体在空中加速下落，加速下落的加速度大小为a，且a＜g（g为重力加速度），在物体下落h高度的过程中，下列说法中正确的是（　　）
A．重力势能减小了mahB．动能增大了mah
C．动能增大了m（g-a）hD．机械能损失了m（g-a）h

分析 质量为m的物体在空中以a的加速度下落，必定受阻力作用，应用动能定理分析即可．

解答 解：A、重力做功等于重力势能的减少量，而W=mgh，故A错误；
B、物体在空中以a的加速度下落，故合力F=ma，由动能定理得，△Ek=Fh=mah，故B正确，C错误；
D、机械能损失为△E=△EP-△EK=m（g-a）h，故D正确．
故选：BD

点评 注意理解功能关系，理解动能定理中各个字母的含义，难度不大，属于基础题．

练习册系列答案
相关题目
1．如图所示，固定在水平面上的光滑平行金属导轨，间距为L，右端接有阻值为R的电阻，空间存在方向竖直、磁感应强度为B的匀强磁场．质量为m、电阻为r的导体棒ab与固定弹簧相连，放在导轨上．初始时刻，弹簧恰处于自然长度．给导体棒水平向右的初速度v0，导体棒开始沿导轨往复运动，最终停在初始位置．在此过程中，导体棒始终与导轨垂直并保持良好接触．已知导体棒的电阻r与定值电阻R的阻值相等，不计导轨电阻，则下列说法中正确的是（　　）
A．导体棒开始运动的初始时刻受到的安培力向左
B．导体棒开始运动的初始时刻导体棒两端的电压U=BLv0
C．导体棒开始运动后速度第一次为零时，系统的弹性势能Ep=$\frac{1}{2}$mv02
D．在金属棒整个运动过程中，电阻R上产生的焦耳热Q=$\frac{1}{4}$mv02
2．下列认识正确的是（　　）
A．以匀加速运动的火车为参考系，牛顿运动定律并不成立，这样的参考系是非惯性的
B．经典力学认为，对同一过程的时间的测量，在不同参考系中是不同的
C．经典力学适用于微观粒子的高速运动
D．量子力学能够很好地描述微观粒子的运动规律
19．如图所示，在高1.5m的光滑平台上有一个质量为2kg的小球被一细线栓在竖直挡板上，球与挡板间有一根被压缩的轻质弹簧，当烧断细线时，小球被弹出，小球离开平台前弹簧已恢复原长，已知小球落地时的速度方向与水平方向成60°角，则弹簧被压缩时具有的弹性势能为（g取10m/s2）（　　）
A．25JB．20JC．15JD．10J
6．如图所示，两个质量都是M=0.4kg的砂箱A、B，并排放在光滑的水平桌面上，一颗质量为m=0.1kg的子弹以v0=140m/s的水平速度射向A，射穿A后，进入B并同B一起运动，测得A、B落地点到桌边缘的水平距离之比为1：2，求子弹刚穿出砂箱A时的速度v1及砂箱A、B离开桌面时的速度是多大？
16．如图所示，质量为m1=3kg的小物块A置于水平面上，A与水平面间的动摩擦因数为μ=0.2，质量为m2=1kg的小物块B用不可伸长的细线悬挂着，细线的另一端系在O点，细线长l=0.5m，处于伸直状态且竖直，A、B可视为质点，它们的水平距离s=2.25m，现A以水平初速度v0=5m/s向右滑动并与B发生弹性正撞，取g=10m/s2，求：
（1）A即将与B碰撞时的速度大小；
（2）碰撞后瞬间A和B的速度大小；
（3）B做圆周运动到最高点时受到细线的拉力．
7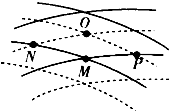．如图所示，实线与虚线分别表示振幅（振幅为A）、频率均相同的两列波的波峰和波谷．此刻M是波峰与波峰的相遇点，下列说法中不正确的是（　　）
A．0、M连线的中点是振动加强的点，其振幅为2A
B．P、N两处的质点始终处在平衡位置
C．随着时间的推移，M处的质点将向O处移动
D．从该时刻起，经过四分之一周期，M处的质点到达平衡位置，此时位移为零
4．有一台发电机产生的感应电动势的瞬时值为e=100$\sqrt{2}$sin100πtV，其内阻为2Ω，若它给阻值为18Ω的电阻供电，则内、外电阻上消耗的功率各为多少？
5．如图，一架在H=2000m的高空以v0=100m/s速度直线飞行的老式轰炸机投放两枚炸弹分别轰炸山脚和山顶的目标A和B，已知山顶高h=1280m，山脚和山顶的目标A和B的水平距离L=800m，不计炸弹受到的空气阻力，g=10m/s2，求：
（1）飞机投第一枚炸弹时离目标A的水平距离
（2）飞机投第一枚炸弹和投第二枚炸弹的时间间隔．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网