题目内容
6. 如图所示,两个质量都是M=0.4kg的砂箱A、B,并排放在光滑的水平桌面上,一颗质量为m=0.1kg的子弹以v0=140m/s的水平速度射向A,射穿A后,进入B并同B一起运动,测得A、B落地点到桌边缘的水平距离之比为1:2,求子弹刚穿出砂箱A时的速度v1及砂箱A、B离开桌面时的速度是多大?
如图所示,两个质量都是M=0.4kg的砂箱A、B,并排放在光滑的水平桌面上,一颗质量为m=0.1kg的子弹以v0=140m/s的水平速度射向A,射穿A后,进入B并同B一起运动,测得A、B落地点到桌边缘的水平距离之比为1:2,求子弹刚穿出砂箱A时的速度v1及砂箱A、B离开桌面时的速度是多大?
分析 A与B都在离开桌面后做平抛运动,由于高度是相等的,所以平抛运动的时间也是相等的,由水平方向的位移关系即可得出速度关系,然后代入动量守恒定律即可求出结果.
解答 解:A与B都在离开桌面后做平抛运动,由于高度是相等的,所以平抛运动的时间t=$\sqrt{\frac{2h}{g}}$也是相等的,水平方向的位移:
x=vt
所以:$\frac{{v}_{A}}{{v}_{B}}=\frac{{x}_{A}}{{x}_{B}}=\frac{1}{2}$ ①
选取向右为正方向,对全过程使用动量守恒定律得:
mv0=MvA+(M+m)vB ②
联立①②得:vA=10m/s,vB=20m/s
子弹射穿A的过程中,有:mv0=mv1+2MvA ③
代入数据得:v1=60m/s
答:子弹刚穿出砂箱A时的速度是60m/s,砂箱A、B离开桌面时的速度分别是10m/s和20m/s.
点评 本题考查了动量守恒定律和平抛运动的综合应用,难度稍大,关键是正确选取系统以及运动的过程.选择全过程法有利于简化解答的过程.

练习册系列答案
相关题目
14. 如图所示,两个质量不同的小球用长度不等的细线拴在同一点,并在同一水平面内作匀速圆周运动,则它们的( )
如图所示,两个质量不同的小球用长度不等的细线拴在同一点,并在同一水平面内作匀速圆周运动,则它们的( )
 如图所示,两个质量不同的小球用长度不等的细线拴在同一点,并在同一水平面内作匀速圆周运动,则它们的( )
如图所示,两个质量不同的小球用长度不等的细线拴在同一点,并在同一水平面内作匀速圆周运动,则它们的( )| A. | 运动周期相同 | B. | 运动线速度一样 | C. | 向心力相同 | D. | 向心加速度相同 |
11.一质量为m的物体在空中加速下落,加速下落的加速度大小为a,且a<g(g为重力加速度),在物体下落h高度的过程中,下列说法中正确的是( )
| A. | 重力势能减小了mah | B. | 动能增大了mah | ||
| C. | 动能增大了m(g-a)h | D. | 机械能损失了m(g-a)h |
2. 一列简谐横波沿x轴正方向传播,传播速度为10m/s.t=0时波传到x=5m处的质点,波形如图所示.则以下判断正确的是 ( )
一列简谐横波沿x轴正方向传播,传播速度为10m/s.t=0时波传到x=5m处的质点,波形如图所示.则以下判断正确的是 ( )
 一列简谐横波沿x轴正方向传播,传播速度为10m/s.t=0时波传到x=5m处的质点,波形如图所示.则以下判断正确的是 ( )
一列简谐横波沿x轴正方向传播,传播速度为10m/s.t=0时波传到x=5m处的质点,波形如图所示.则以下判断正确的是 ( )| A. | 这列波的周期为0.4s | |
| B. | 再经过0.6s,质点P第一次回到平衡位置 | |
| C. | 再经过0.7s,x=9m处的质点Q到达波峰处 | |
| D. | 质点Q到达波峰时,质点P恰好到达波谷处 | |
| E. | 波源开始振动的方向沿y轴的负方向 |
19.入射光照射到某金属表面上发生光电效应,若入射光的强度减弱,而频率保持不变,那么( )
| A. | 从光照射至金属表面上到发射出光电子之间的时间间隔将明显增加 | |
| B. | 逸出的光电子的最大初动能将减小 | |
| C. | 单位时间内从金属表面逸出的光电子数目将减小 | |
| D. | 一定会发生光电效应 |
20. 如图所示,从倾角为θ的足够长的斜面顶端P以速度v0抛出一个小球,落在斜面上某处Q点,小球落在斜面上的速度与斜面的夹角α,若把初速度变为2v0,小球仍落在斜面上,则( )
如图所示,从倾角为θ的足够长的斜面顶端P以速度v0抛出一个小球,落在斜面上某处Q点,小球落在斜面上的速度与斜面的夹角α,若把初速度变为2v0,小球仍落在斜面上,则( )
 如图所示,从倾角为θ的足够长的斜面顶端P以速度v0抛出一个小球,落在斜面上某处Q点,小球落在斜面上的速度与斜面的夹角α,若把初速度变为2v0,小球仍落在斜面上,则( )
如图所示,从倾角为θ的足够长的斜面顶端P以速度v0抛出一个小球,落在斜面上某处Q点,小球落在斜面上的速度与斜面的夹角α,若把初速度变为2v0,小球仍落在斜面上,则( )| A. | 空中的运动时间变为原来的2倍 | B. | 夹角α不变 | ||
| C. | 夹角α将变大 | D. | PQ间距一定是原来间距的2倍 |
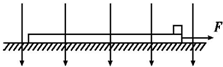 如图所示,长L=1.6m,质量M=3kg的木板静止放在光滑水平面上,质量m=1kg、带电荷量q=+2.5×10-4C的小物块放在木板的右端,木板和物块间的动摩擦因数μ=0.1,所在空间加有一个方向竖直向下,电场强度为E=4.0×104N/C的匀强电场,现对木板施加一水平向右的拉力F.取g=10m/s2,最大静摩擦力等于滑动摩擦力,求:
如图所示,长L=1.6m,质量M=3kg的木板静止放在光滑水平面上,质量m=1kg、带电荷量q=+2.5×10-4C的小物块放在木板的右端,木板和物块间的动摩擦因数μ=0.1,所在空间加有一个方向竖直向下,电场强度为E=4.0×104N/C的匀强电场,现对木板施加一水平向右的拉力F.取g=10m/s2,最大静摩擦力等于滑动摩擦力,求: 如图所示,串联阻值为R的闭合电路中,面积为S的正方形区域abcd存在一个方向垂直纸面向外、磁感应强度均匀增加且变化率为k的匀强磁场Bt,abcd的电阻值也为R,其他电阻不计.电阻两端又向右并联一个平行板电容器.在靠近M板处由静止释放一质量为m、电量为+q的带电粒子(不计重力),经过N板的小孔P进入一个垂直纸面向内、磁感应强度为B的圆形匀强磁场,已知该圆形匀强磁场的半径为r=$\frac{1}{B}$$\sqrt{\frac{mSk}{q}}$.求:
如图所示,串联阻值为R的闭合电路中,面积为S的正方形区域abcd存在一个方向垂直纸面向外、磁感应强度均匀增加且变化率为k的匀强磁场Bt,abcd的电阻值也为R,其他电阻不计.电阻两端又向右并联一个平行板电容器.在靠近M板处由静止释放一质量为m、电量为+q的带电粒子(不计重力),经过N板的小孔P进入一个垂直纸面向内、磁感应强度为B的圆形匀强磁场,已知该圆形匀强磁场的半径为r=$\frac{1}{B}$$\sqrt{\frac{mSk}{q}}$.求: 如图所示,质量为M的小车静止在光滑水平轨道上,下面用长为L的细线悬挂在质量为m的沙箱,一颗质量为m0的子弹以v0的水平速度射入沙箱,并留在其中,在以后运动过程中,求:
如图所示,质量为M的小车静止在光滑水平轨道上,下面用长为L的细线悬挂在质量为m的沙箱,一颗质量为m0的子弹以v0的水平速度射入沙箱,并留在其中,在以后运动过程中,求: