题目内容
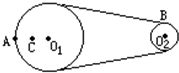 如图所示皮带转动轮,大轮直径是小轮直径的2 倍,A是大轮边缘上一点,B是小轮边缘上一点,C是大轮上一点,C到圆心O1的距离等于小轮半径. 转动时皮带不打滑,则A、B两点的角速度之比ωA:ωB=
如图所示皮带转动轮,大轮直径是小轮直径的2 倍,A是大轮边缘上一点,B是小轮边缘上一点,C是大轮上一点,C到圆心O1的距离等于小轮半径. 转动时皮带不打滑,则A、B两点的角速度之比ωA:ωB=分析:靠传送带传动轮子边缘上的点具有相同的线速度,共轴转动的点具有相同的角速度.根据v=rω,a=ω2r可得出A、B、C三点的角速度之比和向心加速度之比.
解答:解:A、B两点的线速度相等,A的半径是B的半径的2倍,根据v=rω,知ωA:ωB=1:2.
点A、C共轴转动,角速度相等,即ωA:ωC=1:1.所以ωA:ωB:ωC=1:2:1
B、C具有相同的半径,根据a=rω2,知aB:aC=4:1
故答案为:1:2,4:1.
点A、C共轴转动,角速度相等,即ωA:ωC=1:1.所以ωA:ωB:ωC=1:2:1
B、C具有相同的半径,根据a=rω2,知aB:aC=4:1
故答案为:1:2,4:1.
点评:解决本题的关键知道靠传送带传动轮子边缘上的点具有相同的线速度,共轴转动的点具有相同的角速度.掌握线速度与角速度的关系,以及线速度、角速度与向心加速度的关系.

练习册系列答案
 寒假天地重庆出版社系列答案
寒假天地重庆出版社系列答案
相关题目
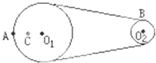 如图所示皮带转动轮,大轮直径是小轮直径的2倍,A是大轮边缘上一点,B是小轮边缘上一点,C是大轮上一点,C到圆心O1的距离等于小轮半径,转动时皮带不打滑,则( )
如图所示皮带转动轮,大轮直径是小轮直径的2倍,A是大轮边缘上一点,B是小轮边缘上一点,C是大轮上一点,C到圆心O1的距离等于小轮半径,转动时皮带不打滑,则( )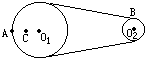 如图所示皮带转动轮,大轮直径是小轮直径的3倍,A是大轮边缘上一点,B是小轮边缘上一点,C是大轮上一点,C到圆心O1的距离等于小轮半径.转动时皮带不打滑,则A、B、C三点的线速度之比vA:vB:vC=
如图所示皮带转动轮,大轮直径是小轮直径的3倍,A是大轮边缘上一点,B是小轮边缘上一点,C是大轮上一点,C到圆心O1的距离等于小轮半径.转动时皮带不打滑,则A、B、C三点的线速度之比vA:vB:vC=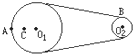 如图所示皮带转动轮,大轮直径是小轮直径的2倍,A是大轮边缘上一点,B是小轮边缘上一点,C是大轮上一点,C到圆心O1的距离等于小轮半径. 转动时皮带不打滑,则( )
如图所示皮带转动轮,大轮直径是小轮直径的2倍,A是大轮边缘上一点,B是小轮边缘上一点,C是大轮上一点,C到圆心O1的距离等于小轮半径. 转动时皮带不打滑,则( )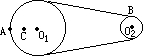 如图所示皮带转动轮,大轮直径是小轮直径的3倍,A是大轮边缘上一点,B是小轮边缘上一点,C是大轮上一点,C到圆心O1的距离等于小轮半径.转动时皮带不打滑,则A、B、C三点的角速度之比ωA:ωB:ωC=
如图所示皮带转动轮,大轮直径是小轮直径的3倍,A是大轮边缘上一点,B是小轮边缘上一点,C是大轮上一点,C到圆心O1的距离等于小轮半径.转动时皮带不打滑,则A、B、C三点的角速度之比ωA:ωB:ωC=