题目内容
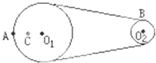 如图所示皮带转动轮,大轮直径是小轮直径的2倍,A是大轮边缘上一点,B是小轮边缘上一点,C是大轮上一点,C到圆心O1的距离等于小轮半径,转动时皮带不打滑,则( )
如图所示皮带转动轮,大轮直径是小轮直径的2倍,A是大轮边缘上一点,B是小轮边缘上一点,C是大轮上一点,C到圆心O1的距离等于小轮半径,转动时皮带不打滑,则( )分析:A和B是通过皮带相连,它们有共同的线速度,A和在C同一个轮上,它们的角速度相等,再有线速度和角速度之间的关系V=rω,就可以判断它们的关系.
解答:解:A、A点与B点通过传送带相连,它们是线速度大小相同,根据v=ωr,可知,因半径的不等,则角速度也不同,故A错误.
B、由VB=rωB,VA=2rωA,又因为VA=VB,ωA=ωC,所以 rωB=2rωC,即ωB=2ωC,所以B错误.
C、A和C在同一个轮上,是同轴转动的,它们的角速度相等,而不是线速度相等,所以C正确.
D、A点与B点通过传送带相连,它们是线速度大小相等,方向不同,所以D错误.
故选:C.
B、由VB=rωB,VA=2rωA,又因为VA=VB,ωA=ωC,所以 rωB=2rωC,即ωB=2ωC,所以B错误.
C、A和C在同一个轮上,是同轴转动的,它们的角速度相等,而不是线速度相等,所以C正确.
D、A点与B点通过传送带相连,它们是线速度大小相等,方向不同,所以D错误.
故选:C.
点评:通过皮带相连的,它们的线速度相等;同轴转的,它们的角速度相等,这是解本题的隐含条件,再有线速度和角速度之间的关系做出判断,考查学生对公式得理解.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
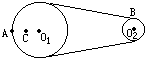 如图所示皮带转动轮,大轮直径是小轮直径的3倍,A是大轮边缘上一点,B是小轮边缘上一点,C是大轮上一点,C到圆心O1的距离等于小轮半径.转动时皮带不打滑,则A、B、C三点的线速度之比vA:vB:vC=
如图所示皮带转动轮,大轮直径是小轮直径的3倍,A是大轮边缘上一点,B是小轮边缘上一点,C是大轮上一点,C到圆心O1的距离等于小轮半径.转动时皮带不打滑,则A、B、C三点的线速度之比vA:vB:vC=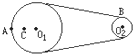 如图所示皮带转动轮,大轮直径是小轮直径的2倍,A是大轮边缘上一点,B是小轮边缘上一点,C是大轮上一点,C到圆心O1的距离等于小轮半径. 转动时皮带不打滑,则( )
如图所示皮带转动轮,大轮直径是小轮直径的2倍,A是大轮边缘上一点,B是小轮边缘上一点,C是大轮上一点,C到圆心O1的距离等于小轮半径. 转动时皮带不打滑,则( )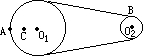 如图所示皮带转动轮,大轮直径是小轮直径的3倍,A是大轮边缘上一点,B是小轮边缘上一点,C是大轮上一点,C到圆心O1的距离等于小轮半径.转动时皮带不打滑,则A、B、C三点的角速度之比ωA:ωB:ωC=
如图所示皮带转动轮,大轮直径是小轮直径的3倍,A是大轮边缘上一点,B是小轮边缘上一点,C是大轮上一点,C到圆心O1的距离等于小轮半径.转动时皮带不打滑,则A、B、C三点的角速度之比ωA:ωB:ωC=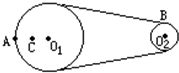 如图所示皮带转动轮,大轮直径是小轮直径的2 倍,A是大轮边缘上一点,B是小轮边缘上一点,C是大轮上一点,C到圆心O1的距离等于小轮半径. 转动时皮带不打滑,则A、B两点的角速度之比ωA:ωB=
如图所示皮带转动轮,大轮直径是小轮直径的2 倍,A是大轮边缘上一点,B是小轮边缘上一点,C是大轮上一点,C到圆心O1的距离等于小轮半径. 转动时皮带不打滑,则A、B两点的角速度之比ωA:ωB=