题目内容
14.如图所示,竖直放置的光滑圆轨道半径为R,A、B为圆轨道内表面的最低点和最高点,在A、B两位置装有压力传感器,可以测量小球经过该位置时对轨道的压力F.一质量为m的小球置于轨道最低点A处,现给小球一水平向右的初速度v,使其沿圆轨道运动;改变小球的初速度v的大小,测量小球在A、B位置对轨道压力FA、FB(小球第1次经过A、B时)的大小,根据测量数据描绘出相应的F-v2图象为相互平行的直线,如图所示.重力加速度为g,求:
(1)图象中v0;
(2)图象中F0;
(3)若圆轨道不光滑,假设小球运动到环的各处时摩擦力大小与速度无关,图中的F0=7mg,改变v的大小,当小球某次经过A时F=9mg,求小球到达B处的速度为多大.
分析 (1)通过v0,F0,对小球在B点应用牛顿第二定律,对A到B的过程应用动能定理即可求解;
(2)对小球在A点应用牛顿第二定律即可求解;
(3)通过牛顿第二定律求得在A、B的速度,然后应用动能定理求得摩擦力做的功;再应用牛顿第二定律求得在A处的速度,然后利用动能定理即可求得在B处的速度.
解答 解:(1)当v=v0时,小球刚好可以到达B点,且在B点的合外力为重力,那么,对小球在B点应用牛顿第二定律,有:$mg=\frac{m{{v}_{B}}^{2}}{R}$;
对小球从A到B应用动能定理得:$-2mgR=\frac{1}{2}m{{v}_{B}}^{2}-\frac{1}{2}m{{v}_{0}}^{2}=\frac{1}{2}mgR-\frac{1}{2}m{{v}_{0}}^{2}$,所以,${v}_{0}=\sqrt{5gR}$;
(2)对小球在A点应用牛顿第二定律,有:${F}_{0}=mg+\frac{m{{v}_{0}}^{2}}{R}=6mg$;
(3)小球运动到环的各处时摩擦力大小与速度无关,那么摩擦力只和位置有关,所以,经过相同位置,摩擦力做功相同;
对小球在A点应用牛顿第二定律,当F0=7mg时有$6mg=\frac{m{{v}_{0}}^{2}}{R}$;
且小球刚好到达B点,对小球在B点应用牛顿第二定律,有:$mg=\frac{m{{v}_{B}}^{2}}{R}$;
对小球从A到B的运动过程应用动能定理可得:$-2mgR+{W}_{f}=\frac{1}{2}m{{v}_{B}}^{2}-\frac{1}{2}m{{v}_{0}}^{2}=-\frac{5}{2}mgR$,所以,${W}_{f}=-\frac{1}{2}mgR$;
当F=9mg时,在A点有:$9mg-mg=8mg=\frac{m{{v}_{A}}^{2}}{R}$;
那么,由动能定理可得:$-2mgR+{W}_{f}=\frac{1}{2}m{v}_{B}{′}^{2}-\frac{1}{2}m{{v}_{A}}^{2}$,所以,$\frac{1}{2}m{v}_{B}{′}^{2}=\frac{3}{2}mgR$,所以,${v}_{B}′=\sqrt{3gR}$;
答:(1)图象中v0为$\sqrt{5gR}$;
(2)图象中F0为6mg;
(3)若圆轨道不光滑,假设小球运动到环的各处时摩擦力大小与速度无关,图中的F0=7mg,改变v的大小,当小球某次经过A时F=9mg,小球到达B处的速度为$\sqrt{3gR}$.
点评 经典力学问题一般先对物体进行受力分析,求得合外力及运动过程做功情况,然后根据牛顿定律、动能定理及几何关系求解.

 寒假天地重庆出版社系列答案
寒假天地重庆出版社系列答案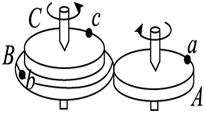 如图所示,B和C是一组塔轮,即B和C半径不同,但固定在同一转动轴上,其半径之比为RB:RC=3:2.A轮的半径大小与C轮相同,它与B轮紧靠在一起,当A轮绕过其中心的竖直轴转动时,由于摩擦作用,B轮也随之无相对滑动地转动起来.a、b、c分别为三轮边缘的三个点,则a、b、c三点在运动过程中的( )
如图所示,B和C是一组塔轮,即B和C半径不同,但固定在同一转动轴上,其半径之比为RB:RC=3:2.A轮的半径大小与C轮相同,它与B轮紧靠在一起,当A轮绕过其中心的竖直轴转动时,由于摩擦作用,B轮也随之无相对滑动地转动起来.a、b、c分别为三轮边缘的三个点,则a、b、c三点在运动过程中的( )| A. | 角速度之比为3:2:2 | B. | 线速度大小之比为3:2:2 | ||
| C. | 向心加速度大小之比为9:6:4 | D. | 转速之比为2:3:2 |
| A. | 苹果自由下落 | B. | 飞机在竖直平面内做匀速圆周运动 | ||
| C. | 标枪在空中飞行 | D. | 小孩沿滑梯匀速滑下 |
| A. | 物体动量方向向上,动量变化量方向向上 | |
| B. | 物体动量方向向上,动量变化量方向向下 | |
| C. | 物体动量方向向下,动量变化量方向向上 | |
| D. | 物体动量方向向下,动量变化量方向向下 |
 放在粗糙水平地面上的滑块,受到随时间t变化的水平拉力F(如图甲所示)作用,其运动的图象如图乙所示,重力加速度g=10m/s2,则下列说法正确的是( )
放在粗糙水平地面上的滑块,受到随时间t变化的水平拉力F(如图甲所示)作用,其运动的图象如图乙所示,重力加速度g=10m/s2,则下列说法正确的是( )| A. | 第1s末滑块所受摩擦力的f的大小为4N | |
| B. | 滑块与水平面间的动摩擦因数μ=0.4 | |
| C. | 1~4s内,力F对滑块做功为48J | |
| D. | 1~4s内,摩擦力对滑块做功为-16J |
 某物体以一定的初速度v0沿倾角为37°的斜面向上滑行,最后又回到出发点,物体与斜面的动摩擦因数恒定,g取10m/s2,在此过程中,其动能Ek随物体到斜面底端距离L的变化关系如图所示,则物体的质量为( )
某物体以一定的初速度v0沿倾角为37°的斜面向上滑行,最后又回到出发点,物体与斜面的动摩擦因数恒定,g取10m/s2,在此过程中,其动能Ek随物体到斜面底端距离L的变化关系如图所示,则物体的质量为( )| A. | 1kg | B. | 2kg | C. | 3kg | D. | 4kg |
| A. | W1-W2+△EP=△EK | B. | W1-W2-△EP=△EK | C. | W1+W2+△EP=△EK |

| A. | 2个力 | B. | 3个力 | C. | 4个力 | D. | 5个力 |
| A. | 在电线上晾晒衣服 | |
| B. | 不以拉扯电线的方式拔出电源插头 | |
| C. | 用湿毛巾擦拭正在照明的白炽灯 | |
| D. | 在同一插座上同时使用多个大功率用电器 |