题目内容
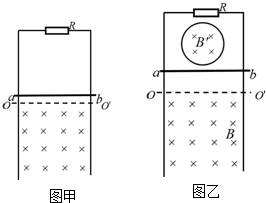
19. 一正方形金属线框位于有界匀强磁场区域内,线框平面与磁场垂直,线框的右边紧贴着磁场边界,如图甲所示.t=0时刻对线框施加一水平向右的外力F,让线框从静止开始做匀加速直线运动穿过磁场.外力F随时间t变化的图线如图乙所示.已知线框质量m=1kg、电阻R=1Ω.以下说法不正确的是( )
一正方形金属线框位于有界匀强磁场区域内,线框平面与磁场垂直,线框的右边紧贴着磁场边界,如图甲所示.t=0时刻对线框施加一水平向右的外力F,让线框从静止开始做匀加速直线运动穿过磁场.外力F随时间t变化的图线如图乙所示.已知线框质量m=1kg、电阻R=1Ω.以下说法不正确的是( )| A. | 做匀加速直线运动的加速度为1m/s2 | |
| B. | 匀强磁场的磁感应强度为2$\sqrt{2}$T | |
| C. | 线框穿过磁场过程中,通过线框的电荷量为$\frac{\sqrt{2}}{2}$C | |
| D. | 线框穿过磁场的过程中,线框上产生的焦耳热为 1.5J |
分析 当t=0时线框的速度为零,没有感应电流,线框不受安培力,根据牛顿第二定律求出加速度a.
由运动学公式求出线框刚出磁场时的速度,得到安培力表达式,由牛顿第二定律即可求出B;
根据法拉第电磁感应定律、欧姆定律结合求解电量.线框通过磁场的过程,由焦耳定律求解热量.
解答 解:A、t=0时刻,线框的速度为零,线框没有感应电流,不受安培力,加速度为 a=$\frac{F}{m}$=$\frac{1}{1}$m/s2=1m/s2
线框的边长为 L=$\frac{1}{2}$at2=$\frac{1}{2}$×1×12m=0.5m
线框刚出磁场时的速度为 v=at=1×1m/s=1m/s
此时线框所受的安培力为FA=BIL,I=$\frac{BLv}{R}$,则得 FA=$\frac{{B}^{2}{L}^{2}v}{R}$,
根据牛顿第二定律得 F-FA=ma,即:F-$\frac{{B}^{2}{L}^{2}v}{R}$=ma,
已知:F=3N,m=1kg,R=1Ω,L=0.5m,v=1m/s,a=1m/s2,
解得:B=2$\sqrt{2}$T,
由q=$\overline{I}$△t,$\overline{I}$=$\frac{\overline{E}}{R}$,$\overline{E}$=$\frac{△Φ}{△t}$,则得通过线框的电量 q=$\frac{△Φ}{R}$=$\frac{B{L}^{2}}{R}$=$\frac{2\sqrt{2}×0.{5}^{2}}{1}$C=$\frac{\sqrt{2}}{2}$C,故ABC正确.
D、线框的位移为 x=L=0.5m,若F=3N保持不变,则F做功为W=Fx=3×0.5J=1.5J,而实际中F的大小逐渐增大,最大为3N,所以F做功应小于1.5J.由于线框加速运动,根据能量守恒得线框上产生的焦耳热小于1.5J,故D错误.
本题选错误的,故选:D.
点评 本题的突破口是根据牛顿第二定律求出加速度,根据运动学公式求出线框的边长和速度,问题就变得简单清晰了,再根据法拉第电磁感应定律、欧姆定律、安培力公式等等电磁感应常用的规律解题.

| A. | 表现为引力且是$\frac{F}{8}$ | B. | 表现为斥力且是$\frac{F}{32}$ | ||
| C. | 表现为斥力且是$\frac{3F}{32}$ | D. | 表现为斥力且是$\frac{F}{8}$ |
 如图所示,带电量为q的正点电荷靠近接地的大金属板,产生类似等量异种电荷产生的电场,点电荷q与金属板间的距离为d,那么点电荷q受到的电场力为( )
如图所示,带电量为q的正点电荷靠近接地的大金属板,产生类似等量异种电荷产生的电场,点电荷q与金属板间的距离为d,那么点电荷q受到的电场力为( )| A. | k$\frac{{q}^{2}}{{d}^{2}}$ | B. | k$\frac{{q}^{2}}{2{d}^{2}}$ | ||
| C. | k$\frac{{q}^{2}}{4{d}^{2}}$ | D. | 以上三个答案均错误 |
 如图,在水平面内有四根相同的均匀光滑金属杆ab、ac、de以及df,其中ab、ac在a点固连,de、df在d点固连,分别构成两个“V”字型导轨,空间中存在垂直于水平面的匀强磁场,用力使导轨edf匀速向右运动,从图示位置开始计时,运动过程中两导轨的角平分线始终重合,导轨间接触始终良好,下列物理量随时间的变化关系正确的是( )
如图,在水平面内有四根相同的均匀光滑金属杆ab、ac、de以及df,其中ab、ac在a点固连,de、df在d点固连,分别构成两个“V”字型导轨,空间中存在垂直于水平面的匀强磁场,用力使导轨edf匀速向右运动,从图示位置开始计时,运动过程中两导轨的角平分线始终重合,导轨间接触始终良好,下列物理量随时间的变化关系正确的是( )| A. |  拉力F与时间t的关系 | B. |  发热功率P与时间t的关系 | ||
| C. |  回路电阻R与时间t的关系 | D. |  电流I与时间t的关系 |
 有一体育娱乐比赛项目,其赛道俯视图如图所示,三根长度均为R的拦阻杆的一端固定在水平面上的O点,并能绕O点以角速度ω逆时针匀速转动,拦阻杆间的夹角为120°.AB为拦阻杆转动平面下方的一段水平传送带,传送带以速度v0匀速运动,方向如图所示,拦阻杆能够拦阻传送带的长度为$\sqrt{3}$R.若参赛者从A端踏上传送带,在传送带上不能与拦阻杆相遇,顺利到达B端即为赢得比赛.则参赛者相对传送带的最小运动速度为( )
有一体育娱乐比赛项目,其赛道俯视图如图所示,三根长度均为R的拦阻杆的一端固定在水平面上的O点,并能绕O点以角速度ω逆时针匀速转动,拦阻杆间的夹角为120°.AB为拦阻杆转动平面下方的一段水平传送带,传送带以速度v0匀速运动,方向如图所示,拦阻杆能够拦阻传送带的长度为$\sqrt{3}$R.若参赛者从A端踏上传送带,在传送带上不能与拦阻杆相遇,顺利到达B端即为赢得比赛.则参赛者相对传送带的最小运动速度为( )| A. | v=$\frac{3\sqrt{3}Rω+2π{v}_{0}}{2π}$ | B. | v=$\frac{3\sqrt{3}Rω+4π{v}_{0}}{4π}$ | C. | v=$\frac{3\sqrt{3}Rω-4π{v}_{0}}{4π}$ | D. | v=$\frac{3\sqrt{3}Rω}{4π}$ |

| A. | 通过L1的电流为L2电流的2倍 | B. | 此时L1、L2和L3的电阻均为12Ω | ||
| C. | L1消耗的电功率为0.75 W | D. | L1消耗的电功率为L2电功率的4倍 |
 如图所示,固定放置的两光滑平行金属导轨,间距d=0.2m,在桌面上的部分是水平的,处在磁感应强度B=0.1T、方向竖直向下的有界磁场中.电阻R=3Ω.桌面高H=0.8m,金属杆ab质量m=0.2kg,电阻r=1Ω,在导轨上距桌面h=0.2m的高处由静止释放,运动过程中a、b两端始终与导轨接触良好并且高度相同.落地点距桌面左边缘的水平距离s=0.4m,g=10m/s2.求:
如图所示,固定放置的两光滑平行金属导轨,间距d=0.2m,在桌面上的部分是水平的,处在磁感应强度B=0.1T、方向竖直向下的有界磁场中.电阻R=3Ω.桌面高H=0.8m,金属杆ab质量m=0.2kg,电阻r=1Ω,在导轨上距桌面h=0.2m的高处由静止释放,运动过程中a、b两端始终与导轨接触良好并且高度相同.落地点距桌面左边缘的水平距离s=0.4m,g=10m/s2.求: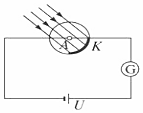 用频率未知的紫外线照射某光电管的阴极时,有光电子飞出.现给你一个电压可调且可指示电压数值的直流电源和一个灵敏度很高的灵敏电流计,试在图的方框中设计一种电路(光电管已画出),要求用该电路测量用所给紫外线照射光电管的阴极时产生的光电子的最大初动能.按照你设计的电路,重要的操作以及需要记录的数据是当加反向电压时,调节滑动触头P,使电流计的示数为零,记录此时电压表的示数U.你所测量的光电子的最大初动能是eU(已知电子电荷量为e).
用频率未知的紫外线照射某光电管的阴极时,有光电子飞出.现给你一个电压可调且可指示电压数值的直流电源和一个灵敏度很高的灵敏电流计,试在图的方框中设计一种电路(光电管已画出),要求用该电路测量用所给紫外线照射光电管的阴极时产生的光电子的最大初动能.按照你设计的电路,重要的操作以及需要记录的数据是当加反向电压时,调节滑动触头P,使电流计的示数为零,记录此时电压表的示数U.你所测量的光电子的最大初动能是eU(已知电子电荷量为e).