题目内容
5. 如图所示,AB为倾角为37°的粗糙斜面,BC为粗糙的水平面,CPD为竖直放置的光滑的半圆轨道,P点为与圆心等高处,已知AB斜面的竖直高度为h=6m,BC的长度为L=8m,一物块在A点由静止释放,物块与AB和BC间的动摩擦因数均为μ=0.1,不考虑经过B点时速度大小的变化,重力加速度大小为g=10m/s2,sin37°=0.6,cos37°=0.8.
如图所示,AB为倾角为37°的粗糙斜面,BC为粗糙的水平面,CPD为竖直放置的光滑的半圆轨道,P点为与圆心等高处,已知AB斜面的竖直高度为h=6m,BC的长度为L=8m,一物块在A点由静止释放,物块与AB和BC间的动摩擦因数均为μ=0.1,不考虑经过B点时速度大小的变化,重力加速度大小为g=10m/s2,sin37°=0.6,cos37°=0.8.(1)若半圆轨道CPD的半径R=1.6m,求物块离开圆轨道后落回到BC上的位置与B点间的距离d;
(2)若物块滑上圆轨道后能沿圆轨道滑下,求R的取值范围.
分析 (1)从A到D对物块运用动能定理,即可求出物块运动到D点的速度,再根据平抛运用规律结合几何关系,即可求出物块离开圆轨道后落回到BC上的位置与B点间的距离d;
(2)物块滑上圆轨道后能沿圆轨道滑下的临界条件为恰好运动$\frac{1}{4}$圆周后速度恰好为0,求出此时半径的临界值即可确定半径R的取值范围.
解答 解:(1)物块恰好通过D点的条件为重力提供向心力,即:mg=m$\frac{{v}^{2}}{R}$,
可得临界速度:v=$\sqrt{gR}$=$\sqrt{10×1.6}$m/s=4m/s
从A到D对物块运用动能定理可得:mg(h-2R)-μmg•$\frac{h}{sinθ}$•cos37°-μmgL=$\frac{1}{2}m{v}_{D}^{2}$-0①
解得:vD=2$\sqrt{6}$>4m/s,故物块可以通过D点,从D点做平抛运动离开圆轨道,
根据平抛运动规律有:x=vDt②
2R=$\frac{1}{2}g{t}^{2}$③
d=L-x④
联立①②③④式可得:d=8-$\frac{8\sqrt{6}}{5}$m≈4.1m
(2)设当半径为R′时,物块运动$\frac{1}{4}$圆周后速度恰好为0,
根据动能定理可得:mg(h-R′)-μmg•$\frac{h}{sinθ}$•cos37°-μmgL=0
解得:R′=2.8m
则物块滑上圆轨道后能沿圆轨道滑下R的取值范围:R≥R′=2.8m
答:(1)若半圆轨道CPD的半径R=1.6m,物块离开圆轨道后落回到BC上的位置与B点间的距离d约为4.1m;
(2)若物块滑上圆轨道后能沿圆轨道滑下,R的取值范围为R≥2.8m.
点评 本题考查动能定理的综合运用,解题关键是要分好运动过程,结合物体运动形式选择合适的规律解题,本题对整个过程运用动能定理,可以化繁为简提高解题效率;第(2)问解决的关键是要找到物块滑上圆轨道后能沿圆轨道滑下的临界条件,即:物块运动$\frac{1}{4}$圆周后速度恰好为0.

 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案| A. | 两球可能相遇 | B. | 两球初速度可能相同 | ||
| C. | 经过B点时两球速度方向可能相同 | D. | 经过B点时两球速度大小可能相等 |
| A. | 一只爬行的蜗牛的动能 | B. | 一个奔跑的孩子的动能 | ||
| C. | 一辆行驶的轿车的动能 | D. | 一架飞行的客机的动能 |
| A. | 合运动的速度一定比分运动的速度大 | |
| B. | 合运动的速度一定比分运动的速度小 | |
| C. | 合运动的速度可能比分运动的速度小 | |
| D. | 两个匀速直线运动的合运动可能是曲线运动 |
| A. | 该同学处于失重状态 | B. | 该同学处于超重状态 | ||
| C. | 该同学的重力变大 | D. | 该同学的重力变小 |
| A. | 红外线传感器 | B. | 气体传感器 | C. | 温度传感器 | D. | 声音传感器 |
| A. | 自由下落的钢珠 | B. | 匀速下落的雨滴 | ||
| C. | 在空中加速上升的火箭 | D. | 在水平路面上转弯的汽车 |
 如图所示,质量为m的物体从高为h,倾角为θ的斜面顶端由静止开始沿斜面下滑,最后停在水平面上,已知物体与斜面、水平面间的动摩擦因数为μ,斜面与平面交接处通过小圆弧平滑连接.求:
如图所示,质量为m的物体从高为h,倾角为θ的斜面顶端由静止开始沿斜面下滑,最后停在水平面上,已知物体与斜面、水平面间的动摩擦因数为μ,斜面与平面交接处通过小圆弧平滑连接.求: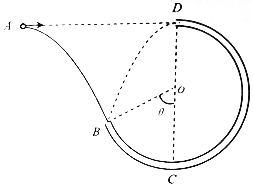 如图所示,一个可视为质点的质量为m=1kg的小球,以某一初速度从A点水平抛出,恰好从竖直圆管BCD的B点沿切线方向进入圆管,经BCD后从圆管的最高点D水平射出,恰好又落到B点.已知圆弧的半径为R=0.3m,且A与D在同一水平线上,BC弧对应的圆心角θ=60°,不计空气阻力,g=10m/s2.求:
如图所示,一个可视为质点的质量为m=1kg的小球,以某一初速度从A点水平抛出,恰好从竖直圆管BCD的B点沿切线方向进入圆管,经BCD后从圆管的最高点D水平射出,恰好又落到B点.已知圆弧的半径为R=0.3m,且A与D在同一水平线上,BC弧对应的圆心角θ=60°,不计空气阻力,g=10m/s2.求: