题目内容
19. 如图,两滑块A、B在光滑水平面上沿同一直线相向运动,滑块A的质量为m,速度大小为2v0,方向向右,滑块B的质量为2m,速度大小为v0,方向向左,求两滑块发生弹性碰撞后的速度.
如图,两滑块A、B在光滑水平面上沿同一直线相向运动,滑块A的质量为m,速度大小为2v0,方向向右,滑块B的质量为2m,速度大小为v0,方向向左,求两滑块发生弹性碰撞后的速度.
分析 两滑块发生弹性碰撞,根据动量守恒定律和机械能守恒定律求出两滑块发生弹性碰撞后的速度大小.
解答 解:规定向右为正方向,设碰后A、B的速度为vA、vB,A、B两滑块组成系统动量守恒,有:
m•2v0-2m•v0=mvA+2mvB
又系统机械能守恒有:
$\frac{1}{2}m•(2{v}_{0})^{2}+\frac{1}{2}•2m{{v}_{0}}^{2}$=$\frac{1}{2}m{{v}_{A}}^{2}+\frac{1}{2}•2m{{v}_{B}}^{2}$
联立以上方程可解得:
vA=-2v0,vB=v0
则碰后A滑块速度水平向左,B滑块速度水平向右
答:两滑块弹性碰撞后的速度分别为2v0、方向向左,v0、方向向右.
点评 本题考查了动量守恒定律和机械能守恒定律的综合运用,知道弹性碰撞过程中,动量守恒、机械能守恒.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
9.把长为0.20m的直导线全部放入匀强磁场中,且保持导线和磁场方向垂直,匀强磁场的磁感应强度为0.1T.当导线中通过的电流为2.0A时,该直导线受到安培力的大小为( )
| A. | 4.0N | B. | 0.4N | C. | 0.04N | D. | 0.0 2N |
7.某物体运动的速度图象如图,根据图象可知( )
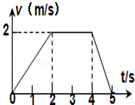

| A. | 0-2s内的加速度为2m/s2 | B. | 0-5s内的位移为10m | ||
| C. | 第1s末与第3s末的速度方向相同 | D. | 第5s末物体回又到出发点 |
14. 如图所示,在倾角θ=30°的光滑固定斜面上,放有两个质量分别为1kg和2kg的可视为质点的小球a和b,两球之间用一根长为L=0.2m的轻杆相连,小球b距水平面的高度h=0.1m.两球由静止开始下滑到光滑水平面上,不计球与水平面碰撞时的机械能损失,取g=10m/s2,下面对系统下滑的整个过程说法正确的是( )
如图所示,在倾角θ=30°的光滑固定斜面上,放有两个质量分别为1kg和2kg的可视为质点的小球a和b,两球之间用一根长为L=0.2m的轻杆相连,小球b距水平面的高度h=0.1m.两球由静止开始下滑到光滑水平面上,不计球与水平面碰撞时的机械能损失,取g=10m/s2,下面对系统下滑的整个过程说法正确的是( )
 如图所示,在倾角θ=30°的光滑固定斜面上,放有两个质量分别为1kg和2kg的可视为质点的小球a和b,两球之间用一根长为L=0.2m的轻杆相连,小球b距水平面的高度h=0.1m.两球由静止开始下滑到光滑水平面上,不计球与水平面碰撞时的机械能损失,取g=10m/s2,下面对系统下滑的整个过程说法正确的是( )
如图所示,在倾角θ=30°的光滑固定斜面上,放有两个质量分别为1kg和2kg的可视为质点的小球a和b,两球之间用一根长为L=0.2m的轻杆相连,小球b距水平面的高度h=0.1m.两球由静止开始下滑到光滑水平面上,不计球与水平面碰撞时的机械能损失,取g=10m/s2,下面对系统下滑的整个过程说法正确的是( )| A. | a球机械能守恒 | B. | b球机械能守恒 | ||
| C. | a球机械能的增加量为0.667J | D. | b球机械能的增加量为0.667J |
 如图所示,一质量为m的带电小球,用长为L的绝缘细线悬挂在水平向右,场强为E的匀强电场中,静止时悬线与竖直方向成θ角,求小球带何种电性及所带电荷量大小.
如图所示,一质量为m的带电小球,用长为L的绝缘细线悬挂在水平向右,场强为E的匀强电场中,静止时悬线与竖直方向成θ角,求小球带何种电性及所带电荷量大小.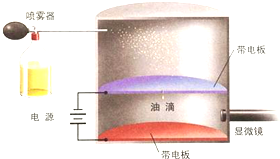 如图所示为密立根用于测量单个电子电荷量的装置.通过喷雾器将细小的油滴喷入某一密闭空间中,这些油滴在喷出时由于与喷雾器产生了摩擦而带电.设油滴的质量为m,带电量为q.由于油滴重力的作用,使少量的油滴通过夹板上的小孔进入了测试设备中.图中两极板间的距离为d.
如图所示为密立根用于测量单个电子电荷量的装置.通过喷雾器将细小的油滴喷入某一密闭空间中,这些油滴在喷出时由于与喷雾器产生了摩擦而带电.设油滴的质量为m,带电量为q.由于油滴重力的作用,使少量的油滴通过夹板上的小孔进入了测试设备中.图中两极板间的距离为d. 质量为m的两个完全相同的光滑小球在挡板作用下静止在倾角为θ的斜面上,重力加速度为g.求:
质量为m的两个完全相同的光滑小球在挡板作用下静止在倾角为θ的斜面上,重力加速度为g.求: 如图所示,水平转台高1.25m,半径为0.2m,可绕通过圆心处的竖直转轴转动,转台的同一半径上放有质量均为0.3kg的小物块A、B(可看成质点),A与转轴间距离为0.1m,B位于转台边缘处,A、B间用长0.1m的细线相连,A、B与水平转台间最大静摩擦力均为0.54N,g取10m/s2.
如图所示,水平转台高1.25m,半径为0.2m,可绕通过圆心处的竖直转轴转动,转台的同一半径上放有质量均为0.3kg的小物块A、B(可看成质点),A与转轴间距离为0.1m,B位于转台边缘处,A、B间用长0.1m的细线相连,A、B与水平转台间最大静摩擦力均为0.54N,g取10m/s2.