题目内容
11. 一质点做简谐运动,其位移和时间关系如图所示.
一质点做简谐运动,其位移和时间关系如图所示.(1)求t=0.25×10-2s时的位移;
(2)在t=1.5×10-2s到2×10-2s的振动过程中,质点的位移、回复力、速度、动能、势能如何变化?
(3)在t=0至8.5×10-2s时间内,质点的路程、位移各多大?
分析 (1)读出振幅和周期,写出振动方程,再求t=0.25×10-2s时的位移;
(2)根据质点位移的库仑,分析各个量的变化情况.
(3)由时间与周期的倍数关系,求解质点通过的路程,得到位移.
解答 解:(1)由题图可知 A=2cm,T=2×10-2s,则ω=$\frac{2π}{T}$=1×102π rad/s
振动方程为x=Asin(ωt-$\frac{π}{2}$)=-Acosωt=-2cos(102π)t cm
当t=0.25×10-2s时,x=-2cos(102π×0.25×10-2)cm=-$\sqrt{2}$cm.
(2)由题图可知在1.5×10-2s~2×10-2s内,质点的位移变大,回复力变大,速度变小,动能变小,势能变大.
(3)从t=0至8.5×10-2s的时间内,因 $\frac{t}{T}$=$\frac{8.5×1{0}^{-2}}{2×1{0}^{-2}}$=4$\frac{1}{4}$=$\frac{17}{4}$
则质点的路程为s=17A=34cm,位移为2 cm.
答:(1)t=0.25×10-2s时的位移是-$\sqrt{2}$cm.
(2)在t=1.5×10-2s到2×10-2s的振动过程中,质点的位移变大,回复力变大,速度变小,动能变小,势能变大.
(3)在t=0至8.5×10-2s时间内,质点的路程为34cm,位移为2 cm.
点评 本题考查运用数学知识处理物理问题的能力,关键要能写出振动方程.书写振动方程抓住三要素:振幅、圆频率和初相位.

练习册系列答案
相关题目
1.有关物体的动量,下列说法正确的是( )
| A. | 某一物体的动量改变,一定是速度大小改变 | |
| B. | 某一物体的动量改变,一定是速度方向改变 | |
| C. | 某一物体的运动速度改变,其动量可能不变 | |
| D. | 物体的运动状态改变,其动量一定改变 |
19.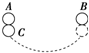 如图所示,半径相同的两个金属小球A、B带有电荷量大小相等的电荷(可视为点电荷),相隔一定的距离,两球之间的相互吸引力大小为F,今用第三个半径相同的不带电的金属小球C先后与A、B两个球接触后移开,这时,A、B两个球之间的相互作用力大小是( )
如图所示,半径相同的两个金属小球A、B带有电荷量大小相等的电荷(可视为点电荷),相隔一定的距离,两球之间的相互吸引力大小为F,今用第三个半径相同的不带电的金属小球C先后与A、B两个球接触后移开,这时,A、B两个球之间的相互作用力大小是( )
 如图所示,半径相同的两个金属小球A、B带有电荷量大小相等的电荷(可视为点电荷),相隔一定的距离,两球之间的相互吸引力大小为F,今用第三个半径相同的不带电的金属小球C先后与A、B两个球接触后移开,这时,A、B两个球之间的相互作用力大小是( )
如图所示,半径相同的两个金属小球A、B带有电荷量大小相等的电荷(可视为点电荷),相隔一定的距离,两球之间的相互吸引力大小为F,今用第三个半径相同的不带电的金属小球C先后与A、B两个球接触后移开,这时,A、B两个球之间的相互作用力大小是( )| A. | $\frac{F}{8}$ | B. | $\frac{F}{4}$ | C. | $\frac{3F}{8}$ | D. | $\frac{3F}{4}$ |
20.如图,一平面简谐波以波速u沿x轴正方形传播,O为坐标原点,已知P点的振动方程为y=Acosωt,则( )
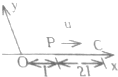

| A. | O点的振动方程为y=Acosω(t-$\frac{1}{u}$) | B. | 波的表达式为y=Acosω[t-($\frac{1}{u}$)-($\frac{x}{u}$)] | ||
| C. | 波的表达式为y=Acosω[t+($\frac{1}{u}$)-($\frac{x}{u}$)] | D. | C点的振动方程为y=Acosω(t-$\frac{3l}{u}$) |
1. 同步卫星在赤道上空同步轨道上定位以后,由于受到太阳、月球及其他天体的引力作用影响,会产生漂移运动而偏离原来的位置,若偏离达到一定程度,就要发动卫星上的小发动机进行修正.如图所示中,A为离地面36000km的同步轨道,B和C为两个已经偏离轨道但仍在赤道平面内做圆周运动的卫星,下列说法正确的是( )
同步卫星在赤道上空同步轨道上定位以后,由于受到太阳、月球及其他天体的引力作用影响,会产生漂移运动而偏离原来的位置,若偏离达到一定程度,就要发动卫星上的小发动机进行修正.如图所示中,A为离地面36000km的同步轨道,B和C为两个已经偏离轨道但仍在赤道平面内做圆周运动的卫星,下列说法正确的是( )
 同步卫星在赤道上空同步轨道上定位以后,由于受到太阳、月球及其他天体的引力作用影响,会产生漂移运动而偏离原来的位置,若偏离达到一定程度,就要发动卫星上的小发动机进行修正.如图所示中,A为离地面36000km的同步轨道,B和C为两个已经偏离轨道但仍在赤道平面内做圆周运动的卫星,下列说法正确的是( )
同步卫星在赤道上空同步轨道上定位以后,由于受到太阳、月球及其他天体的引力作用影响,会产生漂移运动而偏离原来的位置,若偏离达到一定程度,就要发动卫星上的小发动机进行修正.如图所示中,A为离地面36000km的同步轨道,B和C为两个已经偏离轨道但仍在赤道平面内做圆周运动的卫星,下列说法正确的是( )| A. | 开动B的小发动机向前喷气,使B适当减速,可使卫星回到同步轨道 | |
| B. | B的速率大于C的速率 | |
| C. | 开动C的小发动机向前喷气,使C适当减速,可使卫星回到同步轨道 | |
| D. | B的角速度大于C的角速度 |
 如图所示,两带电平行板A、B间的电场为匀强电场,场强为E,两板相距d,板长L.一带电量为q、质量为m的粒子沿平行于板方向从两板的正中间射入电场后向着B板偏转,不计带电粒子所受重力,则
如图所示,两带电平行板A、B间的电场为匀强电场,场强为E,两板相距d,板长L.一带电量为q、质量为m的粒子沿平行于板方向从两板的正中间射入电场后向着B板偏转,不计带电粒子所受重力,则 “测定玻璃的折射率”实验中,下图是在纸上留下的实验痕迹,其中直线a、a′是描在纸上的玻璃砖的两个边.
“测定玻璃的折射率”实验中,下图是在纸上留下的实验痕迹,其中直线a、a′是描在纸上的玻璃砖的两个边. 某同学利用多用电表的电阻档判断二极管的正负极,当红表笔接A端,黑表笔接B端时,电阻很小;当黑表笔接A端,红表笔接B端时,电阻很大,如图所示,则B(填“A”或“B”)端是二极管的正极.
某同学利用多用电表的电阻档判断二极管的正负极,当红表笔接A端,黑表笔接B端时,电阻很小;当黑表笔接A端,红表笔接B端时,电阻很大,如图所示,则B(填“A”或“B”)端是二极管的正极.