题目内容
11.已知月球半径为R0,月球表面处重力加速度为g0.地球和月球的半径之比为$\frac{R}{{R}_{0}}$=4,表面重力加速度之比为$\frac{g}{{g}_{0}}$=6,则地球和月球的密度之比$\frac{ρ}{{ρ}_{0}}$为多少?分析 在星球表面、重力等于万有引力,根据万有引力定律列式求解出质量,由球体体积的表达式和密度定义求解密度表达式进行分析即可.
解答 解:设星球的密度为ρ,由G$\frac{Mm′}{{R}^{2}}$=mg
得GM=gR2,ρ=$\frac{M}{V}$=$\frac{M}{\frac{4}{3}π{R}^{3}}$
联立解得ρ=$\frac{3g}{4GπR}$
设地球、月球的密度分别为ρ、ρ0,则$\frac{ρ}{{ρ}_{0}}=\frac{g{R}_{0}}{{g}_{0}R}$
将$\frac{R}{{R}_{0}}$=4,$\frac{g}{{g}_{0}}$=6代入上式,解得$\frac{ρ}{{ρ}_{0}}$=$\frac{3}{2}$
答:地球和月球的密度之比$\frac{ρ}{{ρ}_{0}}$为$\frac{3}{2}$.
点评 本题关键是明确在星球的表面重力等于万有引力,根据万有引力定律的表达式列式分析即可,基础题目.

练习册系列答案
相关题目
2.关于热力学温标和摄氏温标,下列说法正确的是( )
| A. | 热力学温度与摄氏温度的关系是T=t-273.15K | |
| B. | 热力学温度升高1K大于摄氏温度升高1℃ | |
| C. | 热力学温度升高1K等于摄氏温度升高1℃ | |
| D. | 某物体摄氏温度为10℃,即热力学温度为10K |
6.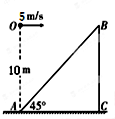 如图所示,斜面与水平面之间的夹角为45°,在斜面底端A点正上方高度为10m处的o点,以5m/s的速度水平抛出一个小球,飞行一段时间后撞在斜面上,这段飞行所用的时间为(g=10m/s2)( )
如图所示,斜面与水平面之间的夹角为45°,在斜面底端A点正上方高度为10m处的o点,以5m/s的速度水平抛出一个小球,飞行一段时间后撞在斜面上,这段飞行所用的时间为(g=10m/s2)( )
 如图所示,斜面与水平面之间的夹角为45°,在斜面底端A点正上方高度为10m处的o点,以5m/s的速度水平抛出一个小球,飞行一段时间后撞在斜面上,这段飞行所用的时间为(g=10m/s2)( )
如图所示,斜面与水平面之间的夹角为45°,在斜面底端A点正上方高度为10m处的o点,以5m/s的速度水平抛出一个小球,飞行一段时间后撞在斜面上,这段飞行所用的时间为(g=10m/s2)( )| A. | 2s | B. | $\sqrt{2}$s | C. | 1s | D. | 0.5s |
16.一条小船在静水中的速度为10m/s,要渡过宽度为60m、水流速度为6m/s的河流,下列说法正确的是( )
| A. | 小船渡河的最短时间为6 s | |
| B. | 小船渡河的最短时间为10 s | |
| C. | 小船渡河的路程最短时,渡河时间为7.5 s | |
| D. | 若小船在静水中的速度增加,则小船渡河的最短路程减小 |
20.下列说法中正确的是( )
| A. | 做曲线运动的物体受到的合外力可以为零 | |
| B. | 在恒力作用下,物体不可能做曲线运动 | |
| C. | 在变力作用下,物体一定做曲线运动 | |
| D. | 曲线运动一定是变速运动 |

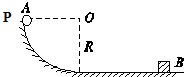 如图,t=0s时小球A从半径为R=0.8m的$\frac{1}{4}$光滑圆弧轨道的上端P点以v0=3m/s的初速度开始滑下,到达光滑水平面上以后,与静止于该水平面上的钢块B发生碰撞,碰撞后小球A被反向弹回,B的质量mB=18kg.A沿原路进入轨道运动恰能上升到它下滑时的出发点(此时速度为零).设A、B碰撞机械能不损失,g取10m/s2,求:
如图,t=0s时小球A从半径为R=0.8m的$\frac{1}{4}$光滑圆弧轨道的上端P点以v0=3m/s的初速度开始滑下,到达光滑水平面上以后,与静止于该水平面上的钢块B发生碰撞,碰撞后小球A被反向弹回,B的质量mB=18kg.A沿原路进入轨道运动恰能上升到它下滑时的出发点(此时速度为零).设A、B碰撞机械能不损失,g取10m/s2,求: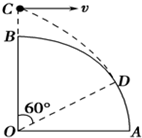 如图所示为四分之一圆柱体OAB的竖直截面,半径为R,在B点上方的C点水平抛出一个小球,小球轨迹恰好在D点与圆柱体相切,OD与OB的夹角为60°.求C点到B点的距离是多少?
如图所示为四分之一圆柱体OAB的竖直截面,半径为R,在B点上方的C点水平抛出一个小球,小球轨迹恰好在D点与圆柱体相切,OD与OB的夹角为60°.求C点到B点的距离是多少?