题目内容
15. 如图,A、C两点分别位于x轴和y轴上,∠OCA=30°,OC的长度为L.在△OCA区域内有垂直于xOy平面向里的匀强磁场,磁感应强度为B.质量为m、电荷量为q的带负电粒子,从坐标原点射入磁场.不计重力.
如图,A、C两点分别位于x轴和y轴上,∠OCA=30°,OC的长度为L.在△OCA区域内有垂直于xOy平面向里的匀强磁场,磁感应强度为B.质量为m、电荷量为q的带负电粒子,从坐标原点射入磁场.不计重力.(1)若粒子沿+y方向射入磁场,当初速度满足什么条件时,粒子在磁场中运动的时间为定值;
(2)大量初速度大小为v=$\frac{qBL}{2m}$的粒子以不同的方向射入第一象限,求从AC边射出的粒子在磁场中运动的最短时间,及该粒子的入射方向与+x的夹角.
分析 (1)粒子转过半圆从OA边射出时时间为定值,速度最大的粒子与AC边相切,画出粒子运动轨迹,根据几何关系求解半径,根据洛伦兹力提供向心力求解最大速度;
(2)要使粒子在磁场中经过的时间最短,需使粒子轨迹对应的弦长最短,所以过O点做垂直于CA的线段为最短的弦,根据几何关系求解圆心角和粒子的入射方向与+x的夹角.
解答 解:粒子转过半圆从OA边射出时时间为定值,速度最大的粒子与AC边相切,如图所示,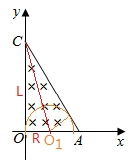
根据几何关系可得:R=Ltan15°=(2-$\sqrt{3}$)L,
根据洛伦兹力提供向心力可得:qvB=m$\frac{{v}^{2}}{R}$,
解得:v=$\frac{qBL}{m}(2-\sqrt{3})$,
所以满足条件的粒子速度范围为:0<v≤$\frac{qBL}{m}(2-\sqrt{3})$;
(2)粒子速度大小相等,要使粒子在磁场中经过的时间最短,需使粒子轨迹对应的弦长最短,所以最短时间的轨迹如图所示,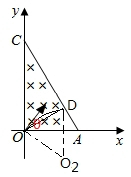
粒子在磁场中的运动半径为:$r=\frac{mv}{qB}=\frac{L}{2}$,
轨迹图中几何关系可得CD=Lsin30°=$\frac{L}{2}$,
由此可知粒子轨迹对应的圆心角为60°;
最短时间为:t=$\frac{60°}{360°}T=\frac{1}{6}×\frac{2πm}{qB}=\frac{πm}{3qB}$,
由图可知,粒子入射方向与+x轴的夹角为$θ=\frac{π}{3}$.
答:(1)若粒子沿+y方向射入磁场,当初速度满足0<v≤$\frac{qBL}{m}(2-\sqrt{3})$时,粒子在磁场中运动的时间为定值;
(2)从AC边射出的粒子在磁场中运动的最短时间为$\frac{πm}{3qB}$,该粒子的入射方向与+x的夹角为$\frac{π}{3}$.
点评 对于带电粒子在磁场中的运动情况分析,一般是确定圆心位置,根据几何关系求半径,结合洛伦兹力提供向心力求解未知量;根据周期公式结合轨迹对应的圆心角求时间.

 名校课堂系列答案
名校课堂系列答案 某电视台玩推箱子的游戏.模型简化如图所示,在动摩擦因素μ=0.2的水平面AB上,某人用水平恒力F推动质量为m=1kg的物体从A点由静止开始作匀加速直线运动,物体到达B点时撤去F,接着又冲上光滑斜面(设经过B点前后速度大小不变),最高能到达C点.用速度传感器测量物体的瞬时速度,并在表格中记录了部分测量数据.求:(g取10m/s2)
某电视台玩推箱子的游戏.模型简化如图所示,在动摩擦因素μ=0.2的水平面AB上,某人用水平恒力F推动质量为m=1kg的物体从A点由静止开始作匀加速直线运动,物体到达B点时撤去F,接着又冲上光滑斜面(设经过B点前后速度大小不变),最高能到达C点.用速度传感器测量物体的瞬时速度,并在表格中记录了部分测量数据.求:(g取10m/s2)| t/s | 0.0 | 0.2 | 0.4 | … | 2.2 | 2.4 | 2.6 | … |
| v/m•s-1 | 0.0 | 0.4 | 0.8 | … | 3.0 | 2.0 | 1.0 | … |
(2)求出物体到达交界面上B点时的速度和时间;
(3)若撤去推力F,在A处给物体一个水平向左的初速度v0,恰能使物体运动到C点,求此初速度v0的大小.
| A. | 在下落过程中,同一时刻二者速度相等 | |
| B. | 甲落地时,乙距地面的高度为H | |
| C. | 甲落地时,乙的速度的大小为$\sqrt{2gH}$ | |
| D. | 甲、乙在空中运动的时间之比为1:2 |
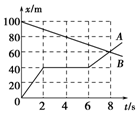
| A. | A物体在2s-6s内做匀速运动,0-2s的加速度大于6s-8s的加速度 | |
| B. | B物体做匀减速直线运动,加速度为-5 m/s2 | |
| C. | A、B两个物体运动8 s时,在距A物体的出发点60 m处相遇 | |
| D. | A、B两个物体开始时相距100 m,同时相向运动 |
 如图所示,取一对用绝缘柱支撑的导体A和B,使它们彼此接触,起初它们不带电,分别贴在导体A、B下部的金属箔均是闭合的.下列关于实验现象描述中正确的是( )
如图所示,取一对用绝缘柱支撑的导体A和B,使它们彼此接触,起初它们不带电,分别贴在导体A、B下部的金属箔均是闭合的.下列关于实验现象描述中正确的是( )| A. | 把带正电荷的物体C移近导体A稳定后,只有A下部的金属箔张开 | |
| B. | 把带正电荷的物体C移近导体A稳定后,只有B下部的金属箔张开 | |
| C. | 把带正电荷的物体C移近导体A后,再把B向右移动稍许使其与A分开,稳定后A、B下部的金属箔都还是张开的 | |
| D. | 把带正电荷的物体C移近导体A后,再把B向右移动稍许使其与A分开,稳定后A、B下部的金属箔都闭合 |
| I/A | 0.12 | 0.21 | 0.29 | 0.34 | 0.38 | 0.42 | 0.45 | 0.47 | 0.49 | 0.50 |
| U/V | 0.20 | 0.40 | 0.60 | 0.80 | 1.00 | 1.20 | 1.40 | 1.60 | 1.80 | 2.00 |
(2)在图乙中画出小灯泡的I-U曲线.分析曲线可知小灯泡的电阻值随U变大而变大 (选填“变大”、“变小”或“不变”);
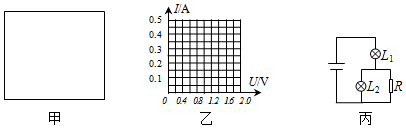
(3)如图丙所示,用一个定值电阻R和两个上述小灯泡组成串并联电路,连接到内阻不计、电动势为1.5V的电源上.已知流过电阻R的电流是流过灯泡L2电流的两倍,则流过灯泡L1的电流约为0.42 A.
 两电荷量分别为q1和q2的点电荷放在x轴上的A、B两点,两电荷连线上各点电势φ随x变化的关系图线如图所示,其中P点电势最低,且AP>BP,则( )
两电荷量分别为q1和q2的点电荷放在x轴上的A、B两点,两电荷连线上各点电势φ随x变化的关系图线如图所示,其中P点电势最低,且AP>BP,则( )| A. | P点电势不为零,场强也不为零 | |
| B. | q1的电荷量大于q2的电荷量 | |
| C. | 负电荷从P点左侧移到P点右侧,电势能先增大后减小 | |
| D. | q1和q2是同种电荷,但不一定是正电荷 |
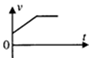
 如图所示,一同学沿一直线行走,现用频闪照相法记录了他行走中9个位置的图片,观察图片,能比较正确地反映该同学运动的速度与时间关系的是( )
如图所示,一同学沿一直线行走,现用频闪照相法记录了他行走中9个位置的图片,观察图片,能比较正确地反映该同学运动的速度与时间关系的是( )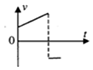


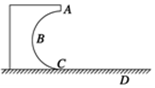 如图所示,一固定在竖直平面内的光滑的半圆形轨道ABC,其半径R=0.5m,轨道在C处与水平地面相切,在C处放一质量等于0.1kg的小物块,给它一水平向左的初速度vo=5m/s,结果它沿CBA运动,通过A点后落在水平地面上的D点.(取重力加速度g=10m/s2,不计空气阻力,以CD水平面为参考平面)求:
如图所示,一固定在竖直平面内的光滑的半圆形轨道ABC,其半径R=0.5m,轨道在C处与水平地面相切,在C处放一质量等于0.1kg的小物块,给它一水平向左的初速度vo=5m/s,结果它沿CBA运动,通过A点后落在水平地面上的D点.(取重力加速度g=10m/s2,不计空气阻力,以CD水平面为参考平面)求: