题目内容
2.弹簧原长为l,劲度系数为k,用力把它缓慢拉到长度为2l,拉力所做的功为W1;继续缓慢拉弹簧,弹簧又增长了l,后阶段拉力所做的功为W2,设整个过程没有超出弹簧的弹性限度.则W1:W2=1:3.分析 拉力做的功等于弹簧增加的弹性势能,弹簧的弹性势能Ep=$\frac{1}{2}$k△l2.
解答 解:弹簧原长为l,劲度系数为k,用力把它缓慢拉到长度为2l,拉力所做的功为W1=$\frac{1}{2}$kl2
继续缓慢拉弹簧,弹簧又增长了l,后阶段拉力所做的功为W2=$\frac{1}{2}$k(2l)2-$\frac{1}{2}$kl2=$\frac{1}{2}$k•3l2
故W1:W2=1:3.
故答案为:1:3.
点评 本题考查弹力做功与弹性势能的关系:弹簧弹力做多少功,弹簧的弹性势能变化多少.

练习册系列答案
 每课必练系列答案
每课必练系列答案
相关题目
12. 一块新手机电池的背面印有如图所示的一些符号,装有该新电池的手机始终处于通话状态最长供电时间为3h,始终处于待机状态最长供电时间为100h.则该手机通话和待机时消耗的平均功率分别约为( )
一块新手机电池的背面印有如图所示的一些符号,装有该新电池的手机始终处于通话状态最长供电时间为3h,始终处于待机状态最长供电时间为100h.则该手机通话和待机时消耗的平均功率分别约为( )
 一块新手机电池的背面印有如图所示的一些符号,装有该新电池的手机始终处于通话状态最长供电时间为3h,始终处于待机状态最长供电时间为100h.则该手机通话和待机时消耗的平均功率分别约为( )
一块新手机电池的背面印有如图所示的一些符号,装有该新电池的手机始终处于通话状态最长供电时间为3h,始终处于待机状态最长供电时间为100h.则该手机通话和待机时消耗的平均功率分别约为( )| A. | 1.8W,5.4×10-2W | B. | 3.6W,0.108W | ||
| C. | 0.6W,1.8×10-2W | D. | 6.48×103W,1.94×102W |
13. 如图所示,甲、乙两物块用跨过定滑轮的轻质细绳连接,分别静止在斜面AB、AC上,滑轮两侧细绳与斜面平行.甲、乙两物块的质量分别为m1、m2.AB斜面粗糙,倾角为α,AC斜面光滑,倾角为β,不计滑轮处摩擦,则以下分析正确的是( )
如图所示,甲、乙两物块用跨过定滑轮的轻质细绳连接,分别静止在斜面AB、AC上,滑轮两侧细绳与斜面平行.甲、乙两物块的质量分别为m1、m2.AB斜面粗糙,倾角为α,AC斜面光滑,倾角为β,不计滑轮处摩擦,则以下分析正确的是( )
 如图所示,甲、乙两物块用跨过定滑轮的轻质细绳连接,分别静止在斜面AB、AC上,滑轮两侧细绳与斜面平行.甲、乙两物块的质量分别为m1、m2.AB斜面粗糙,倾角为α,AC斜面光滑,倾角为β,不计滑轮处摩擦,则以下分析正确的是( )
如图所示,甲、乙两物块用跨过定滑轮的轻质细绳连接,分别静止在斜面AB、AC上,滑轮两侧细绳与斜面平行.甲、乙两物块的质量分别为m1、m2.AB斜面粗糙,倾角为α,AC斜面光滑,倾角为β,不计滑轮处摩擦,则以下分析正确的是( )| A. | 若m1sinα>m2sinβ,则甲所受摩擦力沿斜面向上 | |
| B. | 若在乙物块上面再放一个小物块后,甲、乙仍静止,则甲所受的摩擦力一定变小 | |
| C. | 若在乙物块上面再放一个小物块后,甲、乙仍静止,则甲所受的拉力一定变大 | |
| D. | 若在甲物块上面再放一相、物块后,甲、乙仍静止,则甲所受拉力一定变大 |
7.如图所示是一定质量的理想气体的过程变化图线,下列说法正确的是( )


| A. | 由状态A变化到状态B,气体分子的平均动能减小 | |
| B. | 由状态B变化到状态C,气体分子的平均动能减小 | |
| C. | 由状态A变化到状态C,气体内能随体积均匀增加 | |
| D. | 由A经B到C的过程气体对外做功小于由A经D到C的过程 |
12. 两个相距较近的平行金属板A、B相距为d,接在电压为U的电源上.开关闭合时,质量为m,带电量为-q的油滴恰好静止在两板中点处,如图所示.在保持其他条件不变的情况下,将两板缓慢地水平错开一些,以下说法正确的是( )
两个相距较近的平行金属板A、B相距为d,接在电压为U的电源上.开关闭合时,质量为m,带电量为-q的油滴恰好静止在两板中点处,如图所示.在保持其他条件不变的情况下,将两板缓慢地水平错开一些,以下说法正确的是( )
 两个相距较近的平行金属板A、B相距为d,接在电压为U的电源上.开关闭合时,质量为m,带电量为-q的油滴恰好静止在两板中点处,如图所示.在保持其他条件不变的情况下,将两板缓慢地水平错开一些,以下说法正确的是( )
两个相距较近的平行金属板A、B相距为d,接在电压为U的电源上.开关闭合时,质量为m,带电量为-q的油滴恰好静止在两板中点处,如图所示.在保持其他条件不变的情况下,将两板缓慢地水平错开一些,以下说法正确的是( )| A. | 油滴将向上运动,电流计中的电流从b流向a | |
| B. | 油滴静止不动,电流计中的电流从a流向b | |
| C. | 油滴将下运动,电流计中的电流从a流向b | |
| D. | 油滴静止不动,电流计中无电流流过 |
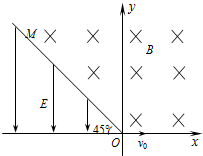 在xOy平面内,直线OM与x轴负方向成45°角,以OM为边界的匀强电场和匀强磁场如图所示.在坐标原点O有一不计重力的粒子,其质量和电荷量分别为m和+q,以v0沿x轴正方向运动,粒子每次到x轴将反弹,第一次无能量损失,以后每次反弹水平分速度不变,竖直分速度大小减半、方向相反.电场强度E和磁感应强度B关系为B=$\frac{m{v}_{0}}{q}$、E=$\frac{m{{v}_{0}}^{2}}{16q}$.求带电粒子:
在xOy平面内,直线OM与x轴负方向成45°角,以OM为边界的匀强电场和匀强磁场如图所示.在坐标原点O有一不计重力的粒子,其质量和电荷量分别为m和+q,以v0沿x轴正方向运动,粒子每次到x轴将反弹,第一次无能量损失,以后每次反弹水平分速度不变,竖直分速度大小减半、方向相反.电场强度E和磁感应强度B关系为B=$\frac{m{v}_{0}}{q}$、E=$\frac{m{{v}_{0}}^{2}}{16q}$.求带电粒子:
 已知单摆的振动图象如图所示
已知单摆的振动图象如图所示