题目内容
13.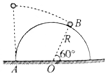 如图所示,一小球从半径为R的固定半圆轨道左端A点正上方某处开始做平抛运动(小球可视为质点),飞行过程中恰好与半圆轨道相切于B点.O点为半圆轨道圆心,OB与水平方向夹角为60°,重力加速度为g,下列说法正确的是( )
如图所示,一小球从半径为R的固定半圆轨道左端A点正上方某处开始做平抛运动(小球可视为质点),飞行过程中恰好与半圆轨道相切于B点.O点为半圆轨道圆心,OB与水平方向夹角为60°,重力加速度为g,下列说法正确的是( )| A. | 小球经B点后将沿着半圆轨道运动 | |
| B. | 小球在B点的加速度为$\frac{g}{2}$ | |
| C. | 小球抛出时的初速度为$\sqrt{\frac{3\sqrt{3}gR}{2}}$ | |
| D. | 小球自抛出至落地点的过程中相同时间内时的变化量不同 |
分析 根据几何知识求出平抛运动到B点的水平位移,结合速度方向,抓住平抛运动某时刻速度方向与水平方向夹角的正切值是位移与水平方向夹角正切值的2倍得出竖直位移,结合平抛运动的规律求出初速度,结合平行四边形定则求出B点的速度.抓住径向的合力提供向心力求出B点支持力为零的速度,确定出小球在B点不受支持力,从而分析判断.
解答 解:由几何知识可得,小球自抛出至B点的水平射程为 x=R+Rcos60°=$\frac{3R}{2}$,
速度方向与水平方向的夹角为30°,设位移与水平方向的夹角为α,则tanα=$\frac{y}{x}=\frac{1}{2}tan30°$,解得平抛运动的竖直位移y=$\frac{\sqrt{3}}{4}R$,
根据y=$\frac{1}{2}g{t}^{2}$,x=v0t得,平抛运动的初速度v0=$\sqrt{\frac{3\sqrt{3}gR}{2}}$,故C正确.
小球在B点的速度${v}_{B}=\frac{{v}_{0}}{cos30°}$=$\sqrt{2\sqrt{3}gR}$,
在B点,若支持力为零,根据$mgcos30°=m\frac{{v}_{B}{′}^{2}}{R}$得,vB′=$\sqrt{\frac{\sqrt{3}gR}{2}}$<vB,可知小球经过B点时,支持力为零,小球在整个过程中做平抛运动,不会验证半圆轨道运动,故A错误.
由于小球在整个过程中做平抛运动,在B点的加速度为g,相等时间内速度变化量相同,故B、D错误.
故选:C.
点评 本题考查了平抛运动、圆周运动与牛顿第二定律的综合运用,通过几何关系和平抛运动的规律求出初速度和B点的速度,通过牛顿第二定律判断B点支持力为零是解决本题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
4.某同学进行体能训练,用了100s时间跑上7楼,试估测他登楼的平均功率最接近的数值是( )
| A. | 10W | B. | 100W | C. | 1kW | D. | 10 kW |
1.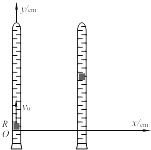 如图所示,一个圆柱形的小红蜡块R在注满清水的竖直密封玻璃管中能以较小的速度v0匀速上浮.当蜡块通过坐标原点O时,使玻璃管沿水平x轴正方向平移,做初速度为零的匀加速直线运动,并从此刻开始计时.t时刻红蜡块的合速度的方向与y轴夹角为α、位移的方向与y夹角为β,则关于红蜡块的运动,下列说法正确的是( )
如图所示,一个圆柱形的小红蜡块R在注满清水的竖直密封玻璃管中能以较小的速度v0匀速上浮.当蜡块通过坐标原点O时,使玻璃管沿水平x轴正方向平移,做初速度为零的匀加速直线运动,并从此刻开始计时.t时刻红蜡块的合速度的方向与y轴夹角为α、位移的方向与y夹角为β,则关于红蜡块的运动,下列说法正确的是( )
 如图所示,一个圆柱形的小红蜡块R在注满清水的竖直密封玻璃管中能以较小的速度v0匀速上浮.当蜡块通过坐标原点O时,使玻璃管沿水平x轴正方向平移,做初速度为零的匀加速直线运动,并从此刻开始计时.t时刻红蜡块的合速度的方向与y轴夹角为α、位移的方向与y夹角为β,则关于红蜡块的运动,下列说法正确的是( )
如图所示,一个圆柱形的小红蜡块R在注满清水的竖直密封玻璃管中能以较小的速度v0匀速上浮.当蜡块通过坐标原点O时,使玻璃管沿水平x轴正方向平移,做初速度为零的匀加速直线运动,并从此刻开始计时.t时刻红蜡块的合速度的方向与y轴夹角为α、位移的方向与y夹角为β,则关于红蜡块的运动,下列说法正确的是( )| A. | 竖直方向分位移y的平方与水平分位移x成正比 | |
| B. | 合速度v的大小随时间t均匀增加 | |
| C. | tanα与时间t成正比 | |
| D. | tanβ与时间t成正比 |
8.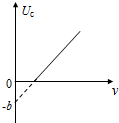 在某次光电效应实验中,得到的遏止电压Uc与入射光的频率v的关系如图所示,若该直线的斜率和纵截距分别为k和-b,电子电荷量的绝对值为e,则( )
在某次光电效应实验中,得到的遏止电压Uc与入射光的频率v的关系如图所示,若该直线的斜率和纵截距分别为k和-b,电子电荷量的绝对值为e,则( )
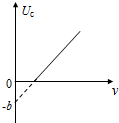 在某次光电效应实验中,得到的遏止电压Uc与入射光的频率v的关系如图所示,若该直线的斜率和纵截距分别为k和-b,电子电荷量的绝对值为e,则( )
在某次光电效应实验中,得到的遏止电压Uc与入射光的频率v的关系如图所示,若该直线的斜率和纵截距分别为k和-b,电子电荷量的绝对值为e,则( )| A. | 普朗克常量可表示为$\frac{k}{e}$ | |
| B. | 若更换材料再实验,得到的图线的k不改变,b改变 | |
| C. | 所用材料的逸出功可表示为eb | |
| D. | b由入射光决定,与所用材料无关 |
18.科学和技术紧密联系在一起的,我们常常重视科学的学习而忽略了技术的学习,实际上技术的进步才是社会发展的真正动力,下面提供了一些技术和原理,其中正确的是( )
| A. | 激光利用光导纤维从一端输入,就可以传到千里之外,实现光纤通信.光纤通信利用的是光的全反射原理 | |
| B. | 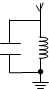 接收无线电波时,所用的调谐电路如图所示,调节电容器的电容时,回路中的振荡电流的频率发生变化,当电台发射电磁波的频率和振荡电流的频率相等时,回路中的振荡电流达到最大,从而接收到该电台 | |
| C. | 当驱动力的频率=系统振动的固有频率时,系统振动振幅最大的现象叫共振.当驱动力的频率与系统振动的固有频率相差较大时,系统振动很小.汽车通常有三级减震系统叫质量-弹簧系统,最下面是由车轮的轴和轮胎组成的第一级质量-弹簧系统,车身和座底弹簧组成第二级质量-弹簧系统,乘客和座椅弹簧组成的第三级质量-弹簧系统,这些质量-弹簧系统的固有频率都比较低,对来自地面的频率较高的振动有减震作用 | |
| D. |  利用光传感器和计算机系统也可以做光的干涉和衍射实验,下面的甲和乙两个图是计算机屏上显示的光照强度分布图,其中甲图是干涉图样,乙图是衍射图样. | |
| E. | 人们利用单摆的等时性,制成了电子钟 |
5.地球同步卫星的运行速率为v1,向心加速度为a1,角速度为ω1,周期为T1;地球赤道上物体随地球自转的速率为v2,向心加速度为a2,角速度为ω2,周期为T2;地球近地卫星的速率为v3,向心加速度为a3,角速度为ω3,周期为T3.则( )
| A. | v3>v1>v2 | B. | a3=a2>a1 | C. | ω3>ω1=ω2 | D. | T3>T1>T2 |
2.一个质量为2kg的物体,在5个共点作用下处于匀速直线运动状态.现同时撤去大小部分别为15N和10N的两个力,其余的力保持不变,关于此后该物体运动的情况说法中正确的是( )
| A. | 可能做匀减速直线运动,加速度大小是2m/s2 | |
| B. | 可能做匀变速圆周运动,向心加速度大小是10m/s2 | |
| C. | 该物体的速度可能先逐渐增大至某一最大值,再逐渐减小 | |
| D. | 该物体的速度可能先逐渐减小至某一非零的最小值,再逐渐增大 |
3.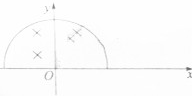 如图所示在x轴上方以原点O为圆心、半径为R的半圆形区域内存在匀强磁场,磁场的方向垂直于xOy平面并指向纸面里,在O点沿y轴正方向不断的向磁场射入速率分别为v1和v2的同种粒子甲、乙,粒子甲平行x轴射出磁场,粒子乙射出磁场后,由第一象限与x轴成30°进入第四象限,不计重力和粒子间的相互作用,则( )
如图所示在x轴上方以原点O为圆心、半径为R的半圆形区域内存在匀强磁场,磁场的方向垂直于xOy平面并指向纸面里,在O点沿y轴正方向不断的向磁场射入速率分别为v1和v2的同种粒子甲、乙,粒子甲平行x轴射出磁场,粒子乙射出磁场后,由第一象限与x轴成30°进入第四象限,不计重力和粒子间的相互作用,则( )
 如图所示在x轴上方以原点O为圆心、半径为R的半圆形区域内存在匀强磁场,磁场的方向垂直于xOy平面并指向纸面里,在O点沿y轴正方向不断的向磁场射入速率分别为v1和v2的同种粒子甲、乙,粒子甲平行x轴射出磁场,粒子乙射出磁场后,由第一象限与x轴成30°进入第四象限,不计重力和粒子间的相互作用,则( )
如图所示在x轴上方以原点O为圆心、半径为R的半圆形区域内存在匀强磁场,磁场的方向垂直于xOy平面并指向纸面里,在O点沿y轴正方向不断的向磁场射入速率分别为v1和v2的同种粒子甲、乙,粒子甲平行x轴射出磁场,粒子乙射出磁场后,由第一象限与x轴成30°进入第四象限,不计重力和粒子间的相互作用,则( )| A. | 甲粒子做圆周运动的半径$\frac{\sqrt{2}}{2}$R | |
| B. | 甲、乙粒子在磁场中运动的时间之比为3:4 | |
| C. | 甲、乙粒子的动能之比为3:1 | |
| D. | 乙粒子通过x轴的坐标为$\sqrt{3}$R |