题目内容
20. 如图所示,质量m=1kg的小物块无初速度地放在倾角为θ=37°的斜面上,物块与斜面间的动摩擦因数μ=0.5.现用大小为F=25N的水平推力作用于物块,求(g取10N、kg,sin37°=0.6,cos37°=0.8)
如图所示,质量m=1kg的小物块无初速度地放在倾角为θ=37°的斜面上,物块与斜面间的动摩擦因数μ=0.5.现用大小为F=25N的水平推力作用于物块,求(g取10N、kg,sin37°=0.6,cos37°=0.8)(1)上滑加速度.
(2)若2s后撤去力F,则物块继续上滑0.8m的位移所需的时间是多少?
分析 根据牛顿第二定律求出物块上滑的加速度.
根据速度时间公式求出2s末的速度,根据牛顿第二定律求出撤去F后向上做匀减速直线运动的加速度,根据位移时间公式求出继续上滑0.8m所需的时间.
解答 解:(1) 根据牛顿第二定律得,
根据牛顿第二定律得,
物块上滑的加速度a=$\frac{Fcos37°-mgsin37°-μ(mgcos37°+Fsin37°)}{m}$=$\frac{25×0.8-10×0.6-0.5×(10×0.8+25×0.6)}{1}$=2.5m/s2.
(2)2s末的速度v1=at1=2.5×2m/s=5m/s,
撤去F后,物体做匀减速直线运动的加速度大小a′=$\frac{mgsin37°+μmgcos37°}{m}$=gsin37°+μgcos37°=6+0.5×8=10m/s2,
根据$x={v}_{1}t-\frac{1}{2}a′{t}^{2}$得,0.8=5t-5t2,
解得t1=0.2s,t2=0.8s(舍去)
答:(1)物体上滑的加速度为2.5m/s2;
(2)物块继续上滑0.8m的位移所需的时间是0.2s.
点评 本题考查了牛顿第二定律和运动学公式的综合运用,知道加速度是联系力学和运动学的桥梁,知道撤去F前后摩擦力的大小不同.

练习册系列答案
相关题目
14.在用游标卡尺观察光的衍射现象时当游标卡尺两测脚间狭缝宽度从0.1mm逐渐增加到0.8mm的过程中,通过狭缝观察一线状光源的情况是( )
| A. | 衍射现象逐渐不明显,最后看不到明显的衍射现象了 | |
| B. | 衍射现象越来越明显 | |
| C. | 衍射条纹的间距随狭缝变宽而逐渐变小 | |
| D. | 衍射条纹的间距随狭缝变宽而逐渐变大 |
8. 如图所示,A、B两物体用轻杆连接,在粗糙的固定斜面上一起沿斜面下滑,已知A、B的质量分别为m1、m2,A、B与斜面间的滑动摩擦因数分别为μ1、μ2,则下列说法正确的是( )
如图所示,A、B两物体用轻杆连接,在粗糙的固定斜面上一起沿斜面下滑,已知A、B的质量分别为m1、m2,A、B与斜面间的滑动摩擦因数分别为μ1、μ2,则下列说法正确的是( )
 如图所示,A、B两物体用轻杆连接,在粗糙的固定斜面上一起沿斜面下滑,已知A、B的质量分别为m1、m2,A、B与斜面间的滑动摩擦因数分别为μ1、μ2,则下列说法正确的是( )
如图所示,A、B两物体用轻杆连接,在粗糙的固定斜面上一起沿斜面下滑,已知A、B的质量分别为m1、m2,A、B与斜面间的滑动摩擦因数分别为μ1、μ2,则下列说法正确的是( )| A. | 无论μ1、μ2的大小关系如何,杆均向下拉B物体 | |
| B. | 无论μ1、μ2的大小关系如何,杆均向上拉B物体 | |
| C. | 若μ1=μ2,则B物体一定受到三个力作用 | |
| D. | 若m1=m2,则B物体一定受到三个力作用 |
5.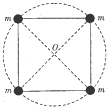 宇宙中存在一些质量相等且离其他恒星较远的四颗星组成的四星系统,通常可忽略其他星体对它们的引力作用.如图,设四星系统中每个星体的质量均为m,半径均为R,四颗星稳定分布在边长为L的正方形的四个顶点上.已知引力常量为G,关于四星系统(忽略星体自转的影响),下列说法正确的是( )
宇宙中存在一些质量相等且离其他恒星较远的四颗星组成的四星系统,通常可忽略其他星体对它们的引力作用.如图,设四星系统中每个星体的质量均为m,半径均为R,四颗星稳定分布在边长为L的正方形的四个顶点上.已知引力常量为G,关于四星系统(忽略星体自转的影响),下列说法正确的是( )
 宇宙中存在一些质量相等且离其他恒星较远的四颗星组成的四星系统,通常可忽略其他星体对它们的引力作用.如图,设四星系统中每个星体的质量均为m,半径均为R,四颗星稳定分布在边长为L的正方形的四个顶点上.已知引力常量为G,关于四星系统(忽略星体自转的影响),下列说法正确的是( )
宇宙中存在一些质量相等且离其他恒星较远的四颗星组成的四星系统,通常可忽略其他星体对它们的引力作用.如图,设四星系统中每个星体的质量均为m,半径均为R,四颗星稳定分布在边长为L的正方形的四个顶点上.已知引力常量为G,关于四星系统(忽略星体自转的影响),下列说法正确的是( )| A. | 四颗星的向心加速度的大小为$\frac{2\sqrt{2}Gm}{{L}^{2}}$ | |
| B. | 四颗星运行的线速度大小是$\sqrt{\frac{Gm(1+2\sqrt{2})}{2\sqrt{2}L}}$ | |
| C. | 四颗星表面的重力加速度均为G$\frac{m}{{R}^{2}}$ | |
| D. | 四颗星的周期均为$\sqrt{\frac{2L}{(2\sqrt{2}+1)Gm}}$ |
9.在电磁学发展过程中,许多科学家做出了贡献.下列说法不正确的是( )
| A. | 奥斯特发现了电流磁效应 | |
| B. | 法拉第发现了电磁感应现象,并首先建立了法拉第电磁感应定律 | |
| C. | 法拉第最先引入“场”的概念,并引入了“场线”来描述“场” | |
| D. | 互感现象是变压器工作的基础 |
 一条船有两岸纤夫拉着沿水平面的笔直水渠前进,水流作用可忽略.岸这边纤夫以恒力F1拉船,方向如图所示.那么,对岸纤夫朝什么方向拉船时,用力最小?最小值为多少?
一条船有两岸纤夫拉着沿水平面的笔直水渠前进,水流作用可忽略.岸这边纤夫以恒力F1拉船,方向如图所示.那么,对岸纤夫朝什么方向拉船时,用力最小?最小值为多少? 如图所示,质量为m=1kg、电荷量为q=5×10-2C的带正电的小滑块,从半径为R=0.4m的光滑绝缘$\frac{1}{4}$圆弧轨道上由静止自A端滑下,整个装置处在方向互相垂直的匀强电场与匀强磁场中.已知E=100V/m,方向水平向右,B=10T,方向垂直纸面向里,g=10m/s2.求:
如图所示,质量为m=1kg、电荷量为q=5×10-2C的带正电的小滑块,从半径为R=0.4m的光滑绝缘$\frac{1}{4}$圆弧轨道上由静止自A端滑下,整个装置处在方向互相垂直的匀强电场与匀强磁场中.已知E=100V/m,方向水平向右,B=10T,方向垂直纸面向里,g=10m/s2.求: