题目内容
19.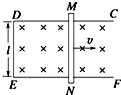 如图所示,固定于水平面上的金属架CDEF处在竖直向下的匀强磁场中,垂直放置的金属棒MN沿框架以速度v向右做匀速运动.t=0时,磁感应强度为B0,此时MN到达的位置使MDEN构成一个边长为l的正方形.
如图所示,固定于水平面上的金属架CDEF处在竖直向下的匀强磁场中,垂直放置的金属棒MN沿框架以速度v向右做匀速运动.t=0时,磁感应强度为B0,此时MN到达的位置使MDEN构成一个边长为l的正方形.(1)若磁感应强度保持不变,则流过金属棒MN的电流方向为N流向M;
(2)为使金属棒MN中不产生感应电流,从t=0开始,磁感应强度B随时间t变化的关系式为B=$\frac{{B}_{0}^{\;}l}{l+vt}$.
分析 (1)根据右手定则,判断流过金属棒MN的电流方向
(2)要使棒不产生感应电流,穿过回路的磁通量应保持不变,根据t=0时刻,回路中磁通量为B0l2,t时刻磁感应强度为B,此时回路中磁通量为Bl(l+vt),
Bl(l+vt)与B0l2 相等,即可求得磁感应强度与时间的关系式.
解答 解:(1)根据右手定则,MN向右运动切割磁感线,产生的感应电流由N流向M
(2)要使棒不产生感应电流,穿过回路的磁通量应保持不变,则有:
B0l2=Bl(l+vt),
解之得:B=$\frac{{B}_{0}^{\;}{l}_{\;}^{2}}{l+vt}$;
故答案为:(1)N流向M;(2)B=$\frac{{{B_0}l}}{l+vt}$
点评 解决本题关键掌握当回路中没有感应电流产生时,回路总的磁通量应保持不变,知道当线圈与磁场垂直时可以用公式Φ=BS求解磁通量.

练习册系列答案
相关题目
14. 如图所示,足够长的U形光滑金属导轨所在平面与水平面成θ角(0<θ<90°),其中MN与PQ平行且间距为L,磁感应强度大小为B的匀强磁场方向垂直导轨所在平面斜向上,导轨电阻不计,金属棒ab由静止开始沿导轨下滑,并与两导轨始终保持垂直且接触良好,棒ab接入电路的电阻为R,当流过棒ab某一横截面的电荷量为q时,棒的速度大小为v,则金属棒ab在此下滑过程中( )
如图所示,足够长的U形光滑金属导轨所在平面与水平面成θ角(0<θ<90°),其中MN与PQ平行且间距为L,磁感应强度大小为B的匀强磁场方向垂直导轨所在平面斜向上,导轨电阻不计,金属棒ab由静止开始沿导轨下滑,并与两导轨始终保持垂直且接触良好,棒ab接入电路的电阻为R,当流过棒ab某一横截面的电荷量为q时,棒的速度大小为v,则金属棒ab在此下滑过程中( )
 如图所示,足够长的U形光滑金属导轨所在平面与水平面成θ角(0<θ<90°),其中MN与PQ平行且间距为L,磁感应强度大小为B的匀强磁场方向垂直导轨所在平面斜向上,导轨电阻不计,金属棒ab由静止开始沿导轨下滑,并与两导轨始终保持垂直且接触良好,棒ab接入电路的电阻为R,当流过棒ab某一横截面的电荷量为q时,棒的速度大小为v,则金属棒ab在此下滑过程中( )
如图所示,足够长的U形光滑金属导轨所在平面与水平面成θ角(0<θ<90°),其中MN与PQ平行且间距为L,磁感应强度大小为B的匀强磁场方向垂直导轨所在平面斜向上,导轨电阻不计,金属棒ab由静止开始沿导轨下滑,并与两导轨始终保持垂直且接触良好,棒ab接入电路的电阻为R,当流过棒ab某一横截面的电荷量为q时,棒的速度大小为v,则金属棒ab在此下滑过程中( )| A. | 受到的安培力方向水平向右 | |
| B. | 下滑位移大小为$\frac{qR}{BL}$ | |
| C. | 运动的加速度大小为gsinθ | |
| D. | 产生的焦耳热为金属棒重力势能的减小量 |
11.2016年9月15日22时13分,“天宫二号”成功发射,经多次轨道控制后,“天宫二号”调整至距地面393公里的预定轨道上,使其正式进入“天宫二号”与神舟十一号载人飞船的交会对接准备阶段.设地球半径为R=6400km,第一宇宙速度为v=7.9km/s,g=9.8m/s2,关于“天宫二号”的下列说法正确的是( )
| A. | 在预定轨道的运行速度一定大于第一宇宙速度v | |
| B. | 进入预定轨道正常运行后舱中物体均处于失重状态 | |
| C. | 可以作为同步通讯卫星使用 | |
| D. | 在预定圆轨道上运行时每天围绕地球转动约15圈 |
8.下列关于电场的叙述中正确的是( )
| A. | 以点电荷为圆心,r为半径的球面上,各点的场强都相同 | |
| B. | 正电荷周围的场强一定比负电荷周围的场强大 | |
| C. | 电场中某点的试探电荷电荷量变为原来两倍,该试探电荷所受电场力不变 | |
| D. | 电荷在电场中某点所受电场力的方向与该点电场的方向可能相反 |
9.某同学在“用打点计时器测速度”的实验中,用打点计时器记录了被小车拖动的纸带的运动情况,在纸带上确定出A、B、C、D、E、F、G共7个计数点.其相邻点间的距离如图1所示,每两个相邻的测量点之间的时间间隔为0.10s.(本题计算结果均保留3位有效数字)

(1)在实验中,使用打点计时器操作步骤应先接通电源再释放纸带(填“释放纸带”或“接通电源”);
(2)每两个计数点间还有4个点没有标出;
(3)试根据纸带上各个计数点间的距离,每隔0.10s测一次速度,计算出打下B、C、D三个点时小车的瞬时速度,并将各个速度值填入表:
(4)如果打A点时开始计时,将B、C、D、E、F各个时刻的瞬时速度标在如图2所示的直角坐标系中,并画出小车的瞬时速度随时间变化的关系图线.

(1)在实验中,使用打点计时器操作步骤应先接通电源再释放纸带(填“释放纸带”或“接通电源”);
(2)每两个计数点间还有4个点没有标出;
(3)试根据纸带上各个计数点间的距离,每隔0.10s测一次速度,计算出打下B、C、D三个点时小车的瞬时速度,并将各个速度值填入表:
| vB | vC | vD | vE | vF | |
| 数值(m/s) | 0.640 | 0.721 |
 如图所示,MN、PQ为足够长的平行导轨,间距L=0.5m.导轨平面与水平面间的夹角θ=37°.NQ⊥MN,NQ间连接有一个R=3Ω的电阻.有一匀强磁场垂直于导轨平面,磁感应强度为B=1T.将一根质量为m=0.05kg的金属棒ab紧靠NQ放置在导轨上,且与导轨接触良好,金属棒的电阻r=2Ω,其余部分电阻不计.现由静止释放金属棒,金属棒沿导轨向下运动过程中始终与NQ平行.已知金属棒与导轨间的动摩擦因数μ=0.5,当金属棒滑行至cd处时速度大小开始保持不变,cd 距离NQ为s=2m.试解答以下问题:(g=10m/s2,sin37°=0.6,cos37°=0.8)
如图所示,MN、PQ为足够长的平行导轨,间距L=0.5m.导轨平面与水平面间的夹角θ=37°.NQ⊥MN,NQ间连接有一个R=3Ω的电阻.有一匀强磁场垂直于导轨平面,磁感应强度为B=1T.将一根质量为m=0.05kg的金属棒ab紧靠NQ放置在导轨上,且与导轨接触良好,金属棒的电阻r=2Ω,其余部分电阻不计.现由静止释放金属棒,金属棒沿导轨向下运动过程中始终与NQ平行.已知金属棒与导轨间的动摩擦因数μ=0.5,当金属棒滑行至cd处时速度大小开始保持不变,cd 距离NQ为s=2m.试解答以下问题:(g=10m/s2,sin37°=0.6,cos37°=0.8)
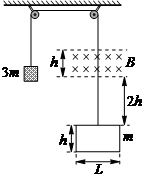 如图所示,质量为3m的重物与一质量为m的线框用一根绝缘细线连接起来,挂在两个高度相同的定滑轮上,已知线框电阻为R,横边边长为L,水平方向匀强磁场的磁感应强度为B,磁场上下边界的距离、线框竖直边长均为h.初始时刻,磁场的下边缘和线框上边缘的高度差为2h,将重物从静止开始释放,线框穿出磁场前,若线框已经做匀速直线运动,滑轮质量、摩擦阻力均不计.求:
如图所示,质量为3m的重物与一质量为m的线框用一根绝缘细线连接起来,挂在两个高度相同的定滑轮上,已知线框电阻为R,横边边长为L,水平方向匀强磁场的磁感应强度为B,磁场上下边界的距离、线框竖直边长均为h.初始时刻,磁场的下边缘和线框上边缘的高度差为2h,将重物从静止开始释放,线框穿出磁场前,若线框已经做匀速直线运动,滑轮质量、摩擦阻力均不计.求: