题目内容
14. 如图所示,在虚线MN上方有一水平向左的匀强电场,场强大小未知,在虚线MN下方有一水平向右的匀强电场,场强大小为E,O是虚线上的一点,一质量为m,带电量为-q的小球从O点开始以初速度v0向左上方运动,小球恰好能做直线运动,方向与水平方向的夹角为θ,当小球回到O点后进入MN下方的电场中运动,并能经过O点正下方的A点,求:
如图所示,在虚线MN上方有一水平向左的匀强电场,场强大小未知,在虚线MN下方有一水平向右的匀强电场,场强大小为E,O是虚线上的一点,一质量为m,带电量为-q的小球从O点开始以初速度v0向左上方运动,小球恰好能做直线运动,方向与水平方向的夹角为θ,当小球回到O点后进入MN下方的电场中运动,并能经过O点正下方的A点,求:(1)MN上方匀强电场的场强E1的大小;
(2)小球从O点出发运动到再次回到O点所用的时间;
(3)小球经过A点时速度的大小.
分析 (1)粒子在MN上方运动时,受重力和向右的电场力,合力沿着轨迹方向,或者说重力和电场力在垂直轨迹方向的分力相等;
(2)根据牛顿第二定律得到加速度,再根据速度时间关系公式列式得到时间;
(3)小球在MN下方的运动过程中,水平分运动是类似竖直上抛运动,竖直分运动是竖直下抛运动,根据分运动公式列式分析.
解答 解:(1)小球做直线运动,有:
qE1sinθ=mgcosθ,
得:${E_1}=\frac{mg}{qtanθ}$;
(2)在MN上方运动时有:F合sinθ=mg,
根据牛顿第二定律,有:F合=ma,
根据速度公式,有:2V0=at1,
得:t1=$\frac{{2{v_0}sinθ}}{g}$;
(3)再次回到O点时:v=v0
水平方向:qE=max,
2v0cosθ=axt2,
到A点时:vx=v0cosθ,
Vy=v0sinθ+gt2,
而${v_A}=\sqrt{v_x^2+v_y^2}$
解得:${v_A}=\frac{v_0}{qE}\sqrt{{q^2}{E^2}+2mgqEsin2θ+4{m^2}{g^2}{{cos}^2}θ}$;
答:(1)MN上方匀强电场的场强E1的大小为$\frac{mg}{qtanθ}$;
(2)小球从O点出发运动到再次回到O点所用的时间为$\frac{{2{v_0}sinθ}}{g}$;
(3)小球经过A点时速度的大小为$\frac{v_0}{qE}\sqrt{{q^2}{E^2}+2mgqEsin2θ+4{m^2}{g^2}{{cos}^2}θ}$.
点评 本题关键是明确小球的受力情况和运动情况,知道匀变速直线运动的条件,并能够结合运动的分解与合成的知识进行分析,不难.

练习册系列答案
相关题目
3. 如图是滑雪场的一条雪道.某同学利用所学知识分析滑雪运动员的运动情况,假设质量为70kg的滑雪运动员(可视为质点)由A点沿弧形雪道滑下,在B点以5根号三的m/s的速度水平飞出,落到了倾斜雪道上的C点(图中未画出).不计空气阻力,Θ=30°,g=10m/s2,则下列判断正确的是( )
如图是滑雪场的一条雪道.某同学利用所学知识分析滑雪运动员的运动情况,假设质量为70kg的滑雪运动员(可视为质点)由A点沿弧形雪道滑下,在B点以5根号三的m/s的速度水平飞出,落到了倾斜雪道上的C点(图中未画出).不计空气阻力,Θ=30°,g=10m/s2,则下列判断正确的是( )
 如图是滑雪场的一条雪道.某同学利用所学知识分析滑雪运动员的运动情况,假设质量为70kg的滑雪运动员(可视为质点)由A点沿弧形雪道滑下,在B点以5根号三的m/s的速度水平飞出,落到了倾斜雪道上的C点(图中未画出).不计空气阻力,Θ=30°,g=10m/s2,则下列判断正确的是( )
如图是滑雪场的一条雪道.某同学利用所学知识分析滑雪运动员的运动情况,假设质量为70kg的滑雪运动员(可视为质点)由A点沿弧形雪道滑下,在B点以5根号三的m/s的速度水平飞出,落到了倾斜雪道上的C点(图中未画出).不计空气阻力,Θ=30°,g=10m/s2,则下列判断正确的是( )| A. | 该滑雪运动员腾空的时间为根号3s | |
| B. | BC两点间的高度差为5m | |
| C. | 运动员落到C点重力的瞬时功率为7kW | |
| D. | 若该滑雪运动员从A点上方更高处滑下,落到倾斜雪道上时速度与竖直方向的夹角变小 |
4.下列关于质点的说法中正确的是( )
| A. | 研究运动员百米赛跑冲刺动作时,运动员可以看作质点 | |
| B. | 研究地球公转时,地球不可以看作质点 | |
| C. | 研究足球运动员踢出的弧线球时,可以将球看作质点 | |
| D. | 研究从北京开往上海的一列火车的运行总时间时,火车可以看作质点 |
2.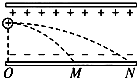 带电粒子P所带的电荷量是带电粒子Q的3倍,它们以相等的速度v0从同一点出发,沿着跟电场强度垂直的方向射入匀强电场,分别打在M、N点,若OM=MN,则P和Q的质量之比为(不计重力为( )
带电粒子P所带的电荷量是带电粒子Q的3倍,它们以相等的速度v0从同一点出发,沿着跟电场强度垂直的方向射入匀强电场,分别打在M、N点,若OM=MN,则P和Q的质量之比为(不计重力为( )
 带电粒子P所带的电荷量是带电粒子Q的3倍,它们以相等的速度v0从同一点出发,沿着跟电场强度垂直的方向射入匀强电场,分别打在M、N点,若OM=MN,则P和Q的质量之比为(不计重力为( )
带电粒子P所带的电荷量是带电粒子Q的3倍,它们以相等的速度v0从同一点出发,沿着跟电场强度垂直的方向射入匀强电场,分别打在M、N点,若OM=MN,则P和Q的质量之比为(不计重力为( )| A. | 3:4 | B. | 4:3 | C. | 3:2 | D. | 2:3 |
9.质量不同、带电量相同的粒子,不计重力,垂直于电力线射入同一个匀强电场.若它们离开电场时速度方向改变的角度相同,则它们在进入电场前必然具有相同的( )
| A. | 速度 | B. | 动量 | C. | 动能 | D. | 速度、动量和动能 |
3. 如图A、B为等量同种电荷,且均为正电荷.M、N、P为A、B连线的中垂线上的三个点,O为连线的中点.则( )
如图A、B为等量同种电荷,且均为正电荷.M、N、P为A、B连线的中垂线上的三个点,O为连线的中点.则( )
 如图A、B为等量同种电荷,且均为正电荷.M、N、P为A、B连线的中垂线上的三个点,O为连线的中点.则( )
如图A、B为等量同种电荷,且均为正电荷.M、N、P为A、B连线的中垂线上的三个点,O为连线的中点.则( )| A. | 将另一点电荷q由M点移到O点过程中,电场力做功为零 | |
| B. | M、N、P、O点的电势满足UM<UN<UP<UO | |
| C. | 在该电场中O点的场强最小 | |
| D. | EM和EP可能大小相等 |

 如图所示,长L=0.20m的丝线的一端拴一质量为m=1.0×10-4 kg、带电荷量为q=+1.0×10-6 C的小球,另一端连在一水平轴O上,整个装置处在竖直向上的匀强电场中,电场强度E=2.0×103 N/C.现将小球拉到与轴O在同一水平面的A点上,然后给小球一个竖直向上的初速度v0,使小球可在竖直面内做圆周运动,取g=10m/s2.求:
如图所示,长L=0.20m的丝线的一端拴一质量为m=1.0×10-4 kg、带电荷量为q=+1.0×10-6 C的小球,另一端连在一水平轴O上,整个装置处在竖直向上的匀强电场中,电场强度E=2.0×103 N/C.现将小球拉到与轴O在同一水平面的A点上,然后给小球一个竖直向上的初速度v0,使小球可在竖直面内做圆周运动,取g=10m/s2.求: 如图所示,长为l绝缘细线拴一电荷量为-q质量为m的小球,处在竖直向下的匀强电场中,给小球在A点水平方向某速度时,小球在竖直平面内以O为圆心做匀速圆周运动,A、B分别为轨迹的最低点和最高点,重力加速度为g.求:
如图所示,长为l绝缘细线拴一电荷量为-q质量为m的小球,处在竖直向下的匀强电场中,给小球在A点水平方向某速度时,小球在竖直平面内以O为圆心做匀速圆周运动,A、B分别为轨迹的最低点和最高点,重力加速度为g.求: