��Ŀ����
8�� ��ͼ��ʾ����Եˮƽ���Ϲ̶���U�ν�������䴮���е���ΪC�ĵ������������Ŀ���ΪL��������ǿ�ų��У��Ÿ�Ӧǿ�ȴ�СΪB������Ϊ��ֱ����ƽ�����ϣ�����Ϊm���㵼��������費�ƣ����ڵ����ϣ��뵼�촹ֱ��ʼ�սӴ����ã��պϿ���S����һˮƽ����F�����㵼�����ʹ�㵼����ɾ�ֹ�����˶����赼���㹻�����Ӵ�����Ħ�����Բ��ƣ���
��ͼ��ʾ����Եˮƽ���Ϲ̶���U�ν�������䴮���е���ΪC�ĵ������������Ŀ���ΪL��������ǿ�ų��У��Ÿ�Ӧǿ�ȴ�СΪB������Ϊ��ֱ����ƽ�����ϣ�����Ϊm���㵼��������費�ƣ����ڵ����ϣ��뵼�촹ֱ��ʼ�սӴ����ã��պϿ���S����һˮƽ����F�����㵼�����ʹ�㵼����ɾ�ֹ�����˶����赼���㹻�����Ӵ�����Ħ�����Բ��ƣ�����1�������������ϻ��۵ĵ�������㵼����ٶȴ�С�Ĺ�ϵ��
��2���㵼������о���s��������ʱ�䣮
���� ��1����E=BLv�����Ӧ�綯�ƣ���Q=CU�����ϵʽ��
��2���ɶ������������������ٶȣ�Ȼ���������غ㶨�������������˶�ʱ�䣮
��� �⣺��1������������ĸ�Ӧ�綯�ƣ�E=BLv��
�������������ϵĵ�ѹ��U=E=BLv��
�����������ϻ��۵ĵ������Q=CU=CE=CBLv �٣�
��2���Ե�������ɶ��������ã�Ft-BILt=mv-0��
Ft-BLQ=mv���ɢٵã�v=$\frac{Ft}{C{B}^{2}{L}^{2}+m}$��
�������غ㶨�ɵģ�Fs=$\frac{1}{2}$mv2+$\frac{1}{2}$CE2��
��ã�t=$\sqrt{\frac{2s��m+C{B}^{2}{L}^{2}��}{F}}$��
�𣺣�1�������������ϻ��۵ĵ�������㵼����ٶȴ�С�Ĺ�ϵΪ��Q=CBLv��
��2���㵼������о���s��������ʱ��Ϊ$\sqrt{\frac{2s��m+C{B}^{2}{L}^{2}��}{F}}$��
���� ���⿼�������������ٶȵĹ�ϵ����������˶�ʱ�䣬�������������˶����̣�Ӧ��E=BLv�����������������غ㶨�ɼ�����ȷ���⣮

��ϰ��ϵ�д�
 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�
�����Ŀ
 �ڡ��õ��ڲⶨ�������ٶȵ�ʵ���С�
�ڡ��õ��ڲⶨ�������ٶȵ�ʵ���С�



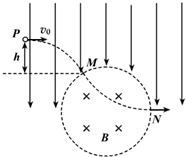 ij�ռ����һ��ֱ���µ���ǿ�糡��Բ���������ǿ�ų����Ÿ�Ӧǿ��ΪB������ֱֽ�������ͼ��ʾ��һ����Ϊm��������Ϊ+q�����ӣ���P����ˮƽ�ٶ�v0����糡�У�Ȼ���M������ų�����N������ų�����֪���������Ӵ�M������ų�ʱ���ٶ�����ֱ�����30��ǣ���MN��Բ�ܳ���$\frac{1}{3}$�������������ƣ���
ij�ռ����һ��ֱ���µ���ǿ�糡��Բ���������ǿ�ų����Ÿ�Ӧǿ��ΪB������ֱֽ�������ͼ��ʾ��һ����Ϊm��������Ϊ+q�����ӣ���P����ˮƽ�ٶ�v0����糡�У�Ȼ���M������ų�����N������ų�����֪���������Ӵ�M������ų�ʱ���ٶ�����ֱ�����30��ǣ���MN��Բ�ܳ���$\frac{1}{3}$�������������ƣ��� ��ͼ��ʾ�Ŀռ�ֲ������������߽����ƽ�У��������ǵ�ѹΪU��ƽ�а�糡��������Ϊ��ǿ�ų����ų��ķ���ֱ�Ϊ��ֱֽ������ʹ�ֱֽ������Ÿ�Ӧǿ�ȴ�С�ֱ�ΪB��2B�������ų�������Ⱦ�Ϊd��һ����Ϊm�������Ϊq�������Ӵ�O1���ɾ�ֹ�ͷţ�ͨ��N��С��O2��ˮƽ��ֱ����ų��������֪���ӵĺ��ʱ������ϵ��$\frac{q}{m}$=$\frac{U}{2{d}^{2}{B}^{2}}$�����ӵ��������Բ��ƣ���
��ͼ��ʾ�Ŀռ�ֲ������������߽����ƽ�У��������ǵ�ѹΪU��ƽ�а�糡��������Ϊ��ǿ�ų����ų��ķ���ֱ�Ϊ��ֱֽ������ʹ�ֱֽ������Ÿ�Ӧǿ�ȴ�С�ֱ�ΪB��2B�������ų�������Ⱦ�Ϊd��һ����Ϊm�������Ϊq�������Ӵ�O1���ɾ�ֹ�ͷţ�ͨ��N��С��O2��ˮƽ��ֱ����ų��������֪���ӵĺ��ʱ������ϵ��$\frac{q}{m}$=$\frac{U}{2{d}^{2}{B}^{2}}$�����ӵ��������Բ��ƣ��� ��ͼ��ʾ������m=4kg����飬�Ӿ�ֹ��ʼ��б�涥���»�����֪б���㹻������Ǧ�=37�㣬�����б���Ķ�Ħ��������=0.2����
��ͼ��ʾ������m=4kg����飬�Ӿ�ֹ��ʼ��б�涥���»�����֪б���㹻������Ǧ�=37�㣬�����б���Ķ�Ħ��������=0.2���� �ڹ̶��ڵ����б���ϴ�ֱ��б�氲����һ�����壬б������Ϊ�ȣ�����Ϊ$\frac{1}{4}$Բ����״���������б���ϣ��뾶�����ȵĹ⻬Բ���ұ����ڼ��뵲��֮�䣬��û����б��Ӵ������ھ�ֹ״̬����ͼ��ʾ����֪������Ϊm���ҵ������Ǽ�2�������ڴ�Բ��O���Լ�ʩ��һƽ����б�����µ�����ʹ����б�淽�������ƶ���ֱ�����뵲��Ӵ�Ϊֹ���赲����ҵ�֧����F1�����ҵ�֧����ΪFN���������ٶ�Ϊg���ڴ˹����У���
�ڹ̶��ڵ����б���ϴ�ֱ��б�氲����һ�����壬б������Ϊ�ȣ�����Ϊ$\frac{1}{4}$Բ����״���������б���ϣ��뾶�����ȵĹ⻬Բ���ұ����ڼ��뵲��֮�䣬��û����б��Ӵ������ھ�ֹ״̬����ͼ��ʾ����֪������Ϊm���ҵ������Ǽ�2�������ڴ�Բ��O���Լ�ʩ��һƽ����б�����µ�����ʹ����б�淽�������ƶ���ֱ�����뵲��Ӵ�Ϊֹ���赲����ҵ�֧����F1�����ҵ�֧����ΪFN���������ٶ�Ϊg���ڴ˹����У��� ��ͬѧ��20�ֶȵ��α꿨�߲����˿��ֱ��ʱ�����ߵĵ�18���̶������α�ĵ�18���̶��߶��루����ʱ������̶��ߣ������ͬѧ�����ĵ���˿��ֱ��Ϊ0.90mm����ͬѧ��ǧ�ֳ߲�������˿��ֱ��ʱ��ͼ��ʾ����ͬѧ�IJ���ֵΪ0.700��0.001mm������Ϊ������ͬѧ���������һ�µ�ԭ���ǣ�ϵͳ��
��ͬѧ��20�ֶȵ��α꿨�߲����˿��ֱ��ʱ�����ߵĵ�18���̶������α�ĵ�18���̶��߶��루����ʱ������̶��ߣ������ͬѧ�����ĵ���˿��ֱ��Ϊ0.90mm����ͬѧ��ǧ�ֳ߲�������˿��ֱ��ʱ��ͼ��ʾ����ͬѧ�IJ���ֵΪ0.700��0.001mm������Ϊ������ͬѧ���������һ�µ�ԭ���ǣ�ϵͳ��