题目内容
3.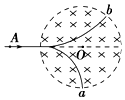 两个质量相同、所带电荷量相等的带电粒子a、b以不同的速率沿着AO方向射入圆形匀强磁场区域,其运动轨迹如图所示.若不计粒子的重力,则下列说法正确的是( )
两个质量相同、所带电荷量相等的带电粒子a、b以不同的速率沿着AO方向射入圆形匀强磁场区域,其运动轨迹如图所示.若不计粒子的重力,则下列说法正确的是( )| A. | b粒子的动能较大 | B. | a粒子带正电,b粒子带负电 | ||
| C. | b粒子在磁场中运动时间较长 | D. | a粒子在磁场中所受洛伦兹力较大 |
分析 a、b两个质量相同、所带电荷量相等的带电粒子以不同的速率对向射入圆形匀强磁场区域,偏转的方向不同,说明受力的方向不同,电性不同,可以根据左手定则判定.从图线来看,a的半径较小,可以结合洛伦兹力提供向心力,写出公式,进行判断,之后,根据公式,再判定动能和运动的时间.
解答 解:A、洛伦兹力提供向心力,即:qvB=m$\frac{{v}^{2}}{r}$,得:r=$\frac{mv}{qB}$,故半径较大的b粒子速度大,动能也大.故A正确.
B、粒子向右运动,根据左手定则,b向上偏转,应当带正电;a向下偏转,应当带负电,故B错误.
C、根据推论公式t=$\frac{θ}{2π}T$、T=$\frac{2πm}{qB}$,周期相等,故磁场中偏转角大的运动的时间也长;a粒子的偏转角大,因此运动的时间就长.故C错误.
D、由公式f=qvB,故速度大的b受洛伦兹力较大.故D错误.
故选:A
点评 该题考查带电粒子在匀强磁场中的偏转,可以结合两个公式进行判定.属于简单题目.

练习册系列答案
相关题目
15.电场中有 A、B 两点,A 点的电势ϕA=-10V;,B 点的电势ϕB=10V,一个电子由 A点运动到 B 点的过程中,下列说法正确的是( )
| A. | 电场力对电子做功 20eV | B. | 电子克服电场力做功 20eV | ||
| C. | 电子的电势能增加了 20eV | D. | 电子的电势能减少了 20eV |
12.一交流电,电压随时间的变化规律如图所示,该交流电压的有效值和周期分别是( )

| A. | 3$\sqrt{2}$V | B. | 0.02s | C. | 0.01s | D. | 3V |
13.雨滴从高空由静止下落,由于空气阻力作用,其加速度逐渐减小,直到变为零,在此过程中雨滴的运动情况是( )
| A. | 速度不断减小,加速度为零时,速度最小 | |
| B. | 速度不断增大,加速度为零时,速度最大 | |
| C. | 位移越来越小 | |
| D. | 速度变化率越来越大 |




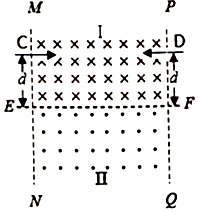 正负电子对撞机是使正负电子以相同速率对撞(撞前速度在同一直线上的碰撞)并进行高能物理研究的实验装置,该装置一般由高能加速器(同步加速器或直线加速器)、环形储存室(把高能加速器在不同时间加速出来的电子束进行积累的环形真空室)和对撞测量区(对撞时发生的新粒子、新现象进行测量)三个部分组成.为了使正负电子在测量区内不同位置进行对撞,在对撞测量区内设置两个方向相反的匀强磁场区域.对撞区域设计的简化原理如图所示:MN和PQ为足够长的竖直边界,水平边界EF将整个区域分成上下两部分,Ⅰ区域的磁场方向垂直纸面向内,Ⅱ区域的磁场方向垂直纸面向外,磁感应强度大小均为B.现有一对正负电子以相同速率分别从注入口C和注入口D同时水平射入,在对撞测量区发生对撞.已知两注入口到EF的距离均为d,边界MN和PQ的间距为L,正电子的质量为m,电量为+e,负电子的质量为m,电量为-e.
正负电子对撞机是使正负电子以相同速率对撞(撞前速度在同一直线上的碰撞)并进行高能物理研究的实验装置,该装置一般由高能加速器(同步加速器或直线加速器)、环形储存室(把高能加速器在不同时间加速出来的电子束进行积累的环形真空室)和对撞测量区(对撞时发生的新粒子、新现象进行测量)三个部分组成.为了使正负电子在测量区内不同位置进行对撞,在对撞测量区内设置两个方向相反的匀强磁场区域.对撞区域设计的简化原理如图所示:MN和PQ为足够长的竖直边界,水平边界EF将整个区域分成上下两部分,Ⅰ区域的磁场方向垂直纸面向内,Ⅱ区域的磁场方向垂直纸面向外,磁感应强度大小均为B.现有一对正负电子以相同速率分别从注入口C和注入口D同时水平射入,在对撞测量区发生对撞.已知两注入口到EF的距离均为d,边界MN和PQ的间距为L,正电子的质量为m,电量为+e,负电子的质量为m,电量为-e.
 一个初速度为零的带正电的粒子电荷量q=10-10C,质量m=10-20kg,经宽度L=8cm,电压U=200V的电场加速后,以水平速度v.穿越一宽度也为L的真空无场区域,沿中心线(图中水平虚线)飞入边长仍为L的正方形电场区域abcd,区域内有平行于ab且竖直向下的匀强电场,场强3750V/m,如图所示,若粒子飞出电场后恰好绕固定在O点的负点电荷Q开始做匀速圆周运动,不计粒子重力,不考虑各部分电场之间的相互影响(静电力常数k=9.0×109N•m2/C2),试求:
一个初速度为零的带正电的粒子电荷量q=10-10C,质量m=10-20kg,经宽度L=8cm,电压U=200V的电场加速后,以水平速度v.穿越一宽度也为L的真空无场区域,沿中心线(图中水平虚线)飞入边长仍为L的正方形电场区域abcd,区域内有平行于ab且竖直向下的匀强电场,场强3750V/m,如图所示,若粒子飞出电场后恰好绕固定在O点的负点电荷Q开始做匀速圆周运动,不计粒子重力,不考虑各部分电场之间的相互影响(静电力常数k=9.0×109N•m2/C2),试求: