题目内容
9. 如图,边长为L的正方形ABCD处在竖直平面内,其中AB边水平、BC边竖直.一带电粒子质量为m、电荷量为-q(重力不计),以水平速度v0从A点射入正方形区域.为使带电粒子能从C点射出正方形区域,可以在正方形ABCD区域内加一个竖直方向的匀强电场,也可以在D点放入一个点电荷,则( )
如图,边长为L的正方形ABCD处在竖直平面内,其中AB边水平、BC边竖直.一带电粒子质量为m、电荷量为-q(重力不计),以水平速度v0从A点射入正方形区域.为使带电粒子能从C点射出正方形区域,可以在正方形ABCD区域内加一个竖直方向的匀强电场,也可以在D点放入一个点电荷,则( )| A. | 匀强电场的方向竖直向上,且电场强度E=$\frac{m{{v}_{0}}^{2}}{qL}$ | |
| B. | 若只加竖直方向的匀强电场,粒子经过C点时的速率为$\sqrt{5}$v0 | |
| C. | 若只在D点放入点电荷,则点电荷应带正电,电荷量为$\frac{m{{v}_{0}}^{2}L}{kq}$ | |
| D. | 只在D点放入点电荷,粒子从A点运动到C点所需时间为$\frac{πL}{4{v}_{0}}$ |
分析 粒子在匀强电场中做类平抛运动,根据运动的合成与分解,垂直电场方向匀速运动,沿电场方向匀加速运动,根据牛顿第二定律运动学公式可以求出带电粒子在匀强电场中的场强,经过C点的速度及运动时间;粒子在点电荷电场中做匀速圆周运动,库仑力提供向心力,可以求出D点的点电荷的电量,在点电荷电场中运动$\frac{1}{4}$周期,在点电荷电场中匀速圆周运动,所以经过C点时速度大小等于初速度v0,结合选项分析求解.
解答 解:A、匀强电场竖直向上,带电粒子受到的电场力向上,做类平抛运动,根据牛顿第二定律qE=ma,得a=$\frac{qE}{m}$ ①
水平方向:L=v0t②
竖直方向:L=$\frac{1}{2}$at2 ③
联立①②③得E=$\frac{2m{v}_{0}^{2}}{qL}$,故A错误;
B、粒子在匀强电场中:水平方向L=v0t④
竖直方向L=vyt=$\frac{{v}_{y}}{2}$t⑤
联立④⑤式得vy=2v0
经过C点时速度vC=$\sqrt{{v}_{0}^{2}+{v}_{y}^{2}}$=$\sqrt{5}$v0,故B正确;
C、在D点放入一点电荷,带电粒子在库仑力作用下做匀速圆周运动,从A到C根据牛顿第二定律,有k$\frac{Qq}{{L}^{2}}$=m$\frac{{v}_{0}^{2}}{L}$
解得:Q=$\frac{m{v}_{0}^{2}L}{kq}$,故C正确;
D、根据匀速圆周运动周期公式T=$\frac{2πL}{{v}_{0}}$,那么粒子在点电荷电场中从A点到C点的时间 t=$\frac{T}{4}$=$\frac{1}{4}×\frac{2πL}{{v}_{0}}$=$\frac{πL{v}_{0}}{2}$,故D错误;
故选:BC.
点评 本题考查带电粒子在电场中的运动,关键是要注意在匀强电场中类平抛运动和点电荷电场中匀速圆周运动的处理方法,根据相应的规律求解.

 阅读快车系列答案
阅读快车系列答案| A. | vm只能为2v,与a1、a2无关 | B. | vm可为许多值,与a1、a2的大小有关 | ||
| C. | a1、a2必须是一定的 | D. | a1、a2必须满足$\frac{{a}_{1}{a}_{2}}{{a}_{1}+{a}_{2}}$=$\frac{v}{t}$ |
 如图所示,带点金属球a固定在绝缘支架上,小球b用丝线悬吊在天花板下,小球质量为m、电荷量为q.现将a向右移近b,当丝线与竖直方向的夹角为θ时,ab连线恰好水平,此时ab间距为r.已知静电力常量为k,则(a、b均可视为点电荷)( )
如图所示,带点金属球a固定在绝缘支架上,小球b用丝线悬吊在天花板下,小球质量为m、电荷量为q.现将a向右移近b,当丝线与竖直方向的夹角为θ时,ab连线恰好水平,此时ab间距为r.已知静电力常量为k,则(a、b均可视为点电荷)( )| A. | a、b一定都带正电荷 | B. | a的电荷量为$\frac{mg{r}^{2}tanθ}{kq}$ | ||
| C. | b受到的电场力为$\frac{mg}{qtanθ}$ | D. | b所在处的电场强度为$\frac{mgsinθ}{q}$ |
 如图所示,用手握住一个玻璃瓶(内装一部分水),玻璃瓶瓶口斜朝上始终静止在手中不动.那么,以下说法中正确的是( )
如图所示,用手握住一个玻璃瓶(内装一部分水),玻璃瓶瓶口斜朝上始终静止在手中不动.那么,以下说法中正确的是( )| A. | 玻璃瓶之所以不掉落,是由于受到了手对它的压力 | |
| B. | 若手握瓶的力增大,瓶子所受到的摩擦力也将增大 | |
| C. | 用手握住瓶子,在向瓶子内注水的过程中,瓶子受到的摩擦力将逐渐增大 | |
| D. | 在向瓶子内注水的过程中,为了保证瓶子不掉落,手握瓶的力一定要增大 |
 甲、乙两个物体从同一地点、沿同一直线同时做直线运动,其中v-t图象如图所示,则( )
甲、乙两个物体从同一地点、沿同一直线同时做直线运动,其中v-t图象如图所示,则( )| A. | 1s时甲和乙相遇 | B. | 2s时甲的速度方向反向 | ||
| C. | 2s~6s内甲相对乙做匀速直线运动 | D. | 4s时乙的加速度为0 |
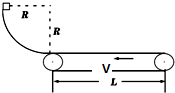 如图所示,一个可视为质点的物块,质量为m=2kg,从光滑四分之一圆弧轨道顶端由静止滑下,到达底端时恰好进入与圆弧轨道底端相切的水平传送带,传送带由一电动机驱动着匀速向左转动,速度大小为v=3m/s.已知圆弧轨道半径R=0.8m,物块与传送带间的动摩擦因数为μ=0.1,两皮带轮之间的距离为L=10m,重力加速度g=10m/s2;求:
如图所示,一个可视为质点的物块,质量为m=2kg,从光滑四分之一圆弧轨道顶端由静止滑下,到达底端时恰好进入与圆弧轨道底端相切的水平传送带,传送带由一电动机驱动着匀速向左转动,速度大小为v=3m/s.已知圆弧轨道半径R=0.8m,物块与传送带间的动摩擦因数为μ=0.1,两皮带轮之间的距离为L=10m,重力加速度g=10m/s2;求: