题目内容
5. 如图所示:真空室内存在匀强磁场,磁场方向垂直于图中纸面向里,磁感应强度的大小B=0.6T,磁场内有一个平面感光板ab板面与磁场方向平行.在距ab的距离为L=16cm处有一个点状α放射源S,它向各个方向发射α粒子,粒子的速度都是v=3.0×106m/s.已知α粒子的电荷量与质量之比$\frac{q}{m}$=5.0×107C/kg.现只考虑到图纸平面中运动的粒子,求:
如图所示:真空室内存在匀强磁场,磁场方向垂直于图中纸面向里,磁感应强度的大小B=0.6T,磁场内有一个平面感光板ab板面与磁场方向平行.在距ab的距离为L=16cm处有一个点状α放射源S,它向各个方向发射α粒子,粒子的速度都是v=3.0×106m/s.已知α粒子的电荷量与质量之比$\frac{q}{m}$=5.0×107C/kg.现只考虑到图纸平面中运动的粒子,求:(1)α粒子的轨道半径和做匀速圆周运动的周期.
(2)ab板上被α粒子打中的区域长度.
分析 带电粒子在磁场中做匀速圆周运动,由洛仑兹力充当向心力可求得粒子的半径,则根据几何关系可求得ab上被打中的区域的长度.
解答 解:(1)α粒子带正电,故在磁场中沿逆时针方向做匀速圆周运动,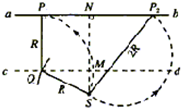
洛伦兹力提供向心力,由牛顿第二定律得:qvB=m$\frac{{v}^{2}}{r}$…①
代入数据解得:r=0.1m=10cm,
α粒子在磁场中做圆周运动的周期:T=$\frac{2πm}{qB}$=$\frac{2π}{5×1{0}^{7}×0.6}$=$\frac{2π}{3}$×10-7s;
(2)由于:2r>l>r,因朝不同方向发射的α粒子的圆轨迹都过S,由此可知,
某一圆轨迹在图中N左侧与ab相切,则此切点P1就是α粒子能打中的左侧最远点.
定出P1点的位置,可作平行于ab的直线cd,cd到ab的距离为r,以S为圆心,r为半径,
作弧交cd于Q点,过Q作ab的垂线,它与ab的交点即为P1,
NP1=$\sqrt{{r}^{2}-(l-r)^{2}}$…②
再考虑N的右侧.任何α粒子在运动中离S的距离不可能超过2R,以2R为半径、S为圆心作圆,交ab于N右侧的P2点,此即右侧能打到的最远点.
由图中几何关系得:NP2=$\sqrt{(2r)^{2}-{l}^{2}}$…③
所求长度为:P1P2=NP1+NP2…④
代入数值得P1P2=20cm,ab上被α粒子打中的区域的长度 P1P2=20cm.
答:(1)α粒子的轨道半径为10cm,做匀速圆周运动的周期为$\frac{2π}{3}$×10-7s.
(2)ab板上被α粒子打中的区域长度为20cm.
点评 带电粒子在磁场中的运动解题的关键在于确定圆心和半径,然后再由几何关系即可求得要求的问题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
13. 如图所示,平行板电容器与电源相连,下极板接地.一带电油滴位于两极板的中心P点且恰好处于静止状态,现将平行板电容器两极板在纸面内绕O′、O迅速顺时针转过45°,则( )
如图所示,平行板电容器与电源相连,下极板接地.一带电油滴位于两极板的中心P点且恰好处于静止状态,现将平行板电容器两极板在纸面内绕O′、O迅速顺时针转过45°,则( )
 如图所示,平行板电容器与电源相连,下极板接地.一带电油滴位于两极板的中心P点且恰好处于静止状态,现将平行板电容器两极板在纸面内绕O′、O迅速顺时针转过45°,则( )
如图所示,平行板电容器与电源相连,下极板接地.一带电油滴位于两极板的中心P点且恰好处于静止状态,现将平行板电容器两极板在纸面内绕O′、O迅速顺时针转过45°,则( )| A. | P点处的电势降低 | |
| B. | 带电油滴仍将保持静止状态 | |
| C. | 带电油滴将水平向右做匀加速直线运动 | |
| D. | 带电油滴到达极板前具有的电势能不断增加 |
20. 如图所示,质量为M的木板静置在光滑的水平面上,在M上放置一质量为m的物块,物块与木板的接触面粗糙.当物块m获得初速度V0而向右滑动时,在滑动过程中下面叙述不正确的是( )
如图所示,质量为M的木板静置在光滑的水平面上,在M上放置一质量为m的物块,物块与木板的接触面粗糙.当物块m获得初速度V0而向右滑动时,在滑动过程中下面叙述不正确的是( )
 如图所示,质量为M的木板静置在光滑的水平面上,在M上放置一质量为m的物块,物块与木板的接触面粗糙.当物块m获得初速度V0而向右滑动时,在滑动过程中下面叙述不正确的是( )
如图所示,质量为M的木板静置在光滑的水平面上,在M上放置一质量为m的物块,物块与木板的接触面粗糙.当物块m获得初速度V0而向右滑动时,在滑动过程中下面叙述不正确的是( )| A. | 若M固定不动,则m对M摩擦力的冲量为零,而M对m的摩擦力做负功 | |
| B. | 若M不固定,则m克服摩擦力做的功全部转化为内能 | |
| C. | 若M不固定,则m对M的摩擦力做功,等于m克服M的摩擦力做功 | |
| D. | 不论M是否固定,m与M相互作用力的冲量总是大小相等、方向相反 |
10. 如图,一个半径为R的导电圆环与一个轴向对称的发散磁场处处正交,环上各点的磁感应强度B大小相等,方向均与环面轴线方向成θ角(环面轴线为竖直方向).若导线环上载有如图所示的恒定电流I,则下列说法正确的是( )
如图,一个半径为R的导电圆环与一个轴向对称的发散磁场处处正交,环上各点的磁感应强度B大小相等,方向均与环面轴线方向成θ角(环面轴线为竖直方向).若导线环上载有如图所示的恒定电流I,则下列说法正确的是( )
 如图,一个半径为R的导电圆环与一个轴向对称的发散磁场处处正交,环上各点的磁感应强度B大小相等,方向均与环面轴线方向成θ角(环面轴线为竖直方向).若导线环上载有如图所示的恒定电流I,则下列说法正确的是( )
如图,一个半径为R的导电圆环与一个轴向对称的发散磁场处处正交,环上各点的磁感应强度B大小相等,方向均与环面轴线方向成θ角(环面轴线为竖直方向).若导线环上载有如图所示的恒定电流I,则下列说法正确的是( )| A. | 导电圆环不受安培力作用 | |
| B. | 导电圆环所受安培力方向竖直向下,大小为2πBIR | |
| C. | 导电圆环所受安培力方向竖直向上,大小为2πBIRsin θ | |
| D. | 导电圆环在水平方向上具有沿半径扩张变大的趋势 |
14.用手握瓶子,瓶子静止在手中,下列说法正确的是( )
| A. | 手对瓶子的摩擦力等于瓶子所受的重力 | |
| B. | 手对瓶子的压力恰好等于瓶子所受的重力 | |
| C. | 手握得越紧,手对瓶子的摩擦力越大 | |
| D. | 手对瓶子的摩擦力必须大于瓶子所受的重力 |
 为测量锂电池的电动势E和内阻r,某同学设计了如图甲所示的电路图.根据测量数据作出$\frac{1}{U}$-$\frac{1}{R}$图象,如图乙所示.若该图线的斜率为k,纵轴截距为b,则该锂电池的电动势E=$\frac{1}{b}$,内阻r=$\frac{k}{b}$(用k、b表示).
为测量锂电池的电动势E和内阻r,某同学设计了如图甲所示的电路图.根据测量数据作出$\frac{1}{U}$-$\frac{1}{R}$图象,如图乙所示.若该图线的斜率为k,纵轴截距为b,则该锂电池的电动势E=$\frac{1}{b}$,内阻r=$\frac{k}{b}$(用k、b表示).
 如图所示,传送带以v=10m/s速度向左匀速运行,AB段长L=2m,竖直平面内的光滑半圆形圆弧槽在B点与水平传送带相切,半圆弧的直径BD=3.2m且B、D连线恰好在竖直方向上,质量m=0.2kg的小滑块与传送带间的动摩擦因数μ=0.5,(g=10m/s2)不计小滑块通过连接处的能量损失.图中OM连线与水平半径OC连线夹角为30°求:
如图所示,传送带以v=10m/s速度向左匀速运行,AB段长L=2m,竖直平面内的光滑半圆形圆弧槽在B点与水平传送带相切,半圆弧的直径BD=3.2m且B、D连线恰好在竖直方向上,质量m=0.2kg的小滑块与传送带间的动摩擦因数μ=0.5,(g=10m/s2)不计小滑块通过连接处的能量损失.图中OM连线与水平半径OC连线夹角为30°求: 如图,长为L=2m、质量mA=4kg的木板A放在光滑水平面上,质量mB=1kg的小物块(可视为质点)位于A的中点,水平力F作用于A.AB间的动摩擦因素μ=0.2(AB间最大静摩擦力等于滑动摩擦力,g=10m/s2).求:
如图,长为L=2m、质量mA=4kg的木板A放在光滑水平面上,质量mB=1kg的小物块(可视为质点)位于A的中点,水平力F作用于A.AB间的动摩擦因素μ=0.2(AB间最大静摩擦力等于滑动摩擦力,g=10m/s2).求: