题目内容
15. 如图所示,在光滑水平面内建立直角坐标系xOy,一质点在该平面内O点受沿x正方向、大小为F的力的作用由静止开始做匀加速直线运动.经过时间t,质点运动到A点,A、O两点间的距离为L;在A点作用力突然变为沿y轴正方向,大小仍为F,再经过时间t,质点运动到B点;在B点将作用力的方向始终与速度方向垂直且改变作用力的大小,使质点在平面内以L为半径、圆心为O,做匀速圆周运动.求:
如图所示,在光滑水平面内建立直角坐标系xOy,一质点在该平面内O点受沿x正方向、大小为F的力的作用由静止开始做匀加速直线运动.经过时间t,质点运动到A点,A、O两点间的距离为L;在A点作用力突然变为沿y轴正方向,大小仍为F,再经过时间t,质点运动到B点;在B点将作用力的方向始终与速度方向垂直且改变作用力的大小,使质点在平面内以L为半径、圆心为O,做匀速圆周运动.求:(1)质点的质量m;
(2)质点做圆周运动的向心力F2;
(3)从B点开始计时,质点运动至距y轴最远的距离L2及所用的时间t2.
分析 (1)质点从O到A做匀加速直线运动,从A到B做类平抛运动,从B到C做匀速圆周运动.研究OA过程,由牛顿第二定律和位移公式结合求出质点的质量m.
(2)研究AB过程,运用运动的分解法,由牛顿第二定律和分速度公式求出质点到达B点的速度,再由向心力公式Fn=m$\frac{{v}^{2}}{L}$求向心力F2.
(3)质点运动至距y轴最远时速度与y轴正方向平行,由几何关系得出距y轴最远的距离L2,进而求所用的时间t2.
解答 解:(1)从O到A物体做匀加速运动,在此过程中,由牛顿第二定律:
F=ma
由运动学得:L=$\frac{1}{2}a{t}^{2}$
联立解得:m=$\frac{F{t}^{2}}{2L}$
(2)质点到达A点的速度设为v,则有:L=$\frac{v}{2}t$
可得:v=$\frac{2L}{t}$
从A到B质点做类平抛运动,在x方向做匀速直线运动,在y方向做匀加速直线运动,加速度为:a=$\frac{F}{m}$=$\frac{2L}{{t}^{2}}$
到达B点时,沿y轴方向的分速度为:vy=at=$\frac{2L}{t}$
所以到达B点的速度为:vB=$\sqrt{{v}^{2}+{v}_{y}^{2}}$=$\frac{2\sqrt{2}L}{t}$,方向与x轴正方向成45°角.
质点做圆周运动的向心力为:F2=m$\frac{{v}_{B}^{2}}{L}$=4F
(3)质点运动至距y轴最远时速度与y轴正方向平行,由几何关系得:
质点距y轴最远的距离为:L2=L+vt+L(1-cos45°)=(4-$\frac{\sqrt{2}}{2}$)L
所用的时间为:t2=$\frac{\frac{π}{4}•L}{{v}_{{B}_{\;}}}$=$\frac{\sqrt{2}πt}{16}$
答:(1)质点的质量m是$\frac{F{t}^{2}}{2L}$;
(2)质点做圆周运动的向心力F2是4F.
(3)从B点开始计时,质点运动至距y轴最远的距离L2是(4-$\frac{\sqrt{2}}{2}$)L,所用的时间t2是$\frac{\sqrt{2}πt}{16}$.
点评 解决本题的关键要明确质点的运动过程,采用程序法分析,要知道质点经历了匀加速直线运动、类平抛运动、匀速圆周运动,结合牛顿第二定律和运动学公式灵活进行研究.

 阅读快车系列答案
阅读快车系列答案| U(V) | 0.0 | 0.2 | 0.5 | 1.0 | 1.5 | 2.0 | 2.5 | 3.0 |
| I(A) | 0.000 | 0.050 | 0.100 | 0.150 | 0.180 | 0.195 | 0.205 | 0.215 |
(1)在如图1框中画出实验电路图.可用的器材有:电压表、电流表、滑线变阻器(变化范围0-10Ω)、电源、小灯泡、电键、导线若干.

(2)在图2中画出小灯泡的U-I曲线.
(3)如图3所示,用一个定值电阻R和两个上述小灯泡组成串并联电路,连接到内阻不计、电动势为3V的电源上.已知流过电阻R的电流是流过灯泡b电流的两倍,则流过灯泡b的电流约为0.07A.
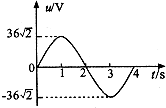 矩形线框在匀强磁场内匀速转动过程中,线框输出的交流电压随时间变化的图象如图所示,下列说法中正确的是( )
矩形线框在匀强磁场内匀速转动过程中,线框输出的交流电压随时间变化的图象如图所示,下列说法中正确的是( )| A. | 交流电压的有效值为36$\sqrt{2}$V | |
| B. | 交流电压的最大值为36$\sqrt{2}$V,频率为50Hz | |
| C. | 2s末线框平面垂直于磁场,通过线框的磁通量最大 | |
| D. | 1s末线框平面垂直于磁场,通过线框的磁通量变化最快 |
 如图所示,MN和PQ是电阻不计的平行金属导轨,其间距为L,导轨弯曲部分光滑,平直部分粗糙,二者平滑连接.右端接一个阻值为R的定值电阻.平直部分导轨左边区域有宽度为d、方向竖直向上、磁感应强度大小为B的匀强磁场.质量为m、电阻也为R的金属棒从高度为h处静止释放,到达磁场右边界处恰好停止.已知金属棒与平直部分导轨间的动摩擦因数为μ,金属棒与导轨间接触良好.则金属棒穿过磁场区域的过程中( )
如图所示,MN和PQ是电阻不计的平行金属导轨,其间距为L,导轨弯曲部分光滑,平直部分粗糙,二者平滑连接.右端接一个阻值为R的定值电阻.平直部分导轨左边区域有宽度为d、方向竖直向上、磁感应强度大小为B的匀强磁场.质量为m、电阻也为R的金属棒从高度为h处静止释放,到达磁场右边界处恰好停止.已知金属棒与平直部分导轨间的动摩擦因数为μ,金属棒与导轨间接触良好.则金属棒穿过磁场区域的过程中( )| A. | 金属棒的最大电压为$\frac{1}{2}$BL$\sqrt{2gh}$ | |
| B. | 金属在磁场中的运动时间为$\frac{\sqrt{2}d}{\sqrt{gh}}$ | |
| C. | 克服安培力所做的功为mgh | |
| D. | 右端的电阻R产生的焦耳热为$\frac{1}{2}$(mgh-μmgd) |
| A. | 人在船上行走时,人对地的速度大于船对地的速度 | |
| B. | 人在船上行走时,人对地的速度小于船对地的速度 | |
| C. | 当人停止时,因船的惯性大,所以船要继续后退 | |
| D. | 人和船组成的系统动量守恒,且总动量等于零,所以人停止船也停止 |
 如图所示,X是未知放射源,M是电场,L是薄铝片,D是计数器.现将强电场M移开,计数器所记录的计数率保侍不变,其后再将薄铝片L移开,则见计数率大幅度上升,则X为( )
如图所示,X是未知放射源,M是电场,L是薄铝片,D是计数器.现将强电场M移开,计数器所记录的计数率保侍不变,其后再将薄铝片L移开,则见计数率大幅度上升,则X为( )| A. | 纯β放射源 | B. | 纯γ放射源 | ||
| C. | α及β的混合放射源 | D. | α及γ的混合放射源 |
 如图,用细线线拴住质量分别为m1、m2的小球a、b并悬挂在天花板下,平衡时两球心在同一水平面上且距天花板的距离为L.将a拉至水平位置后由静止释放,在最低位置时与b发生弹性正碰,若碰后两球上升的最大高度相同.重力加速度为g.求:m1与m2的比值及碰后两球各自的速度大小.
如图,用细线线拴住质量分别为m1、m2的小球a、b并悬挂在天花板下,平衡时两球心在同一水平面上且距天花板的距离为L.将a拉至水平位置后由静止释放,在最低位置时与b发生弹性正碰,若碰后两球上升的最大高度相同.重力加速度为g.求:m1与m2的比值及碰后两球各自的速度大小. 如图所示的电路中,当开关S闭合时,小灯泡A1立刻(填“逐渐”或“立刻”)亮;然后当开关断开时,小灯泡中的电流方向是向右(选填“向左”或“向右”).
如图所示的电路中,当开关S闭合时,小灯泡A1立刻(填“逐渐”或“立刻”)亮;然后当开关断开时,小灯泡中的电流方向是向右(选填“向左”或“向右”).