题目内容
2.海王星是太阳系行星中离地球最远的行星,若已知海王星半径是地球半径的4倍,质量是地球质量的16倍,到太阳的距离是日地间距离的25倍.地球半径为R1,其表面重力加速度是g,引力常量为G.求:(1)海王星的第一宇宙速度;
(2)海王星的密度.
分析 (1)分别由万有引力提供向心力求地球和海王星的第一宇宙速度,再由物体的重力等于万有引力,联立解得海王星的第一宇宙速度;
(2)由在地球表面上物体的重力等于万有引力列式,根据海王星半径是地球半径的4倍,质量是地球质量的16倍,由密度公式可求.
解答 解:(1)设地球的第一宇宙速度为v1,设地球的质量为M,则由牛顿第二定律可得:G$\frac{Mm}{{R}_{1}^{2}}$=m$\frac{{v}_{1}^{2}}{{R}_{1}}$
设海王星的第一宇宙速度为v2,设海王星的质量为M′,G$\frac{{M}^{′}m}{{R}_{2}^{2}}$=m$\frac{{v}_{2}^{2}}{{R}_{2}}$
在地球表面上,物体的重力等于万有引力,有:G$\frac{Mm}{{R}_{1}^{2}}$=mg
又因为海王星半径是地球半径的4倍,质量是地球质量的16倍,
联立解得:v2=2$\sqrt{g{R}_{1}}$
(2)在地球表面上,物体的重力等于万有引力,有:G$\frac{Mm}{{R}_{1}^{2}}$=mg
解得地球质量为:M=$\frac{g{R}_{1}^{2}}{G}$
又因为海王星半径是地球半径的4倍,质量是地球质量的16倍,
所以:ρ=$\frac{{M}^{′}}{V}$=$\frac{16×\frac{g{R}_{1}^{2}}{G}}{\frac{4}{3}π(4{R}_{1})^{3}}$=$\frac{3g}{16Gπ{R}_{1}}$
答:(1)海王星的第一宇宙速度为2$\sqrt{g{R}_{1}}$;
(2)海王星的密度为$\frac{3g}{16Gπ{R}_{1}}$.
点评 利用万有引力定律解答天体运动的问题注意:
两条思路:①在星球表面上,物体的重力等于万有引力;②万有引力提供向心力;
一个黄金代换:GM=gR2;
本题中海王星到太阳的距离是日地间距离的25倍,这一条件是多余的.

 如图所示,利用倾角为α的传送带把一个质量为m的木箱匀速传送L距离,这时木箱升高h,木箱和传送带始终保持相对静止,木箱与传送带间的动摩擦因数为μ,重力加速度为g,关于此过程,下列说法正确的是( )
如图所示,利用倾角为α的传送带把一个质量为m的木箱匀速传送L距离,这时木箱升高h,木箱和传送带始终保持相对静止,木箱与传送带间的动摩擦因数为μ,重力加速度为g,关于此过程,下列说法正确的是( )| A. | 木箱克服摩擦力做功mgh | B. | 摩擦力对木箱做功为mgh | ||
| C. | 摩擦力对木箱做功为零 | D. | 摩擦力对木箱做功为μmgLcosα |
| A. | 0.6小时 | B. | 1.6小时 | C. | 4.0小时 | D. | 24小时 |
 如图所示,一质量为m的小球置于半径为R的光滑竖直圆轨道最低点A处,B为轨道最高点,C、D为圆的水平直径两端点.轻质弹簧的一端固定在圆心O点,另一端与小球栓接,已知弹簧的劲度系数为k=$\frac{mg}{R}$,原长为L=2R,弹簧始终处于弹性限度内,若给小球一水平初速度v0,已知重力加速度为g,则( )
如图所示,一质量为m的小球置于半径为R的光滑竖直圆轨道最低点A处,B为轨道最高点,C、D为圆的水平直径两端点.轻质弹簧的一端固定在圆心O点,另一端与小球栓接,已知弹簧的劲度系数为k=$\frac{mg}{R}$,原长为L=2R,弹簧始终处于弹性限度内,若给小球一水平初速度v0,已知重力加速度为g,则( )| A. | 无论v0多大,小球均不会离开圆轨道 | |
| B. | 若在$\sqrt{2gR}$<v0<$\sqrt{5gR}$则小球会在B、D间脱离圆轨道 | |
| C. | 只要v0>$\sqrt{4gR}$,小球就能做完整的圆周运动 | |
| D. | 只要小球能做完整圆周运动,则小球与轨道间最大压力与最小压力之差与v0无关 |
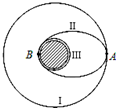 “嫦娥一号”在西昌卫星发射中心发射升空,准确进入预定轨道.随后,“嫦娥一号”经过变轨和制动成功进入环月轨道.如图所示,阴影部分表示月球,设想飞船在圆形轨道Ⅰ上作匀速圆周运动,在圆轨道Ⅰ上飞行n圈所用时间为t到达A点时经过暂短的点火变速,进入椭圆轨道Ⅱ,在到达轨道Ⅱ近月点B点时再次点火变速,进入近月圆形轨道Ⅲ,而后飞船在轨道Ⅲ上绕月球作匀速圆周运动,在圆轨道Ⅲ上飞行n圈所用时间为$\frac{t}{8}$.不考虑其它星体对飞船的影响,求:
“嫦娥一号”在西昌卫星发射中心发射升空,准确进入预定轨道.随后,“嫦娥一号”经过变轨和制动成功进入环月轨道.如图所示,阴影部分表示月球,设想飞船在圆形轨道Ⅰ上作匀速圆周运动,在圆轨道Ⅰ上飞行n圈所用时间为t到达A点时经过暂短的点火变速,进入椭圆轨道Ⅱ,在到达轨道Ⅱ近月点B点时再次点火变速,进入近月圆形轨道Ⅲ,而后飞船在轨道Ⅲ上绕月球作匀速圆周运动,在圆轨道Ⅲ上飞行n圈所用时间为$\frac{t}{8}$.不考虑其它星体对飞船的影响,求: 如图所示,在探究向心力公式的实验中,为了探究物体质量、圆周运动的半径、角速度与向心力的关系,运用的实验方法是控制变量法.现将小球分别放在两边的槽内,为探究小球受到的向心力大小与角速度大小的关系,做法正确的是:在小球运动半径相等(填“相等”或“不相等”)的情况下,用质量相同(填“相同”或“不相同”)的钢球做实验.
如图所示,在探究向心力公式的实验中,为了探究物体质量、圆周运动的半径、角速度与向心力的关系,运用的实验方法是控制变量法.现将小球分别放在两边的槽内,为探究小球受到的向心力大小与角速度大小的关系,做法正确的是:在小球运动半径相等(填“相等”或“不相等”)的情况下,用质量相同(填“相同”或“不相同”)的钢球做实验. 如图所示是游乐园内某种过山车的示意图.半径为R=5.0m的光滑圆形轨道固定在倾角为θ=37°的斜轨道面上的A点,圆轨道的最高点D与车(视为质点)的初始位置P点平齐,B为圆轨道的最低点,C点与圆心O等高,圆轨道与斜轨道PA之间平滑连接.小车从P点由静止开始下滑,恰好到达C点.已知g=10m/s2,sin37°=0.6,cos37°=0.8,车的质量m=100kg.求:
如图所示是游乐园内某种过山车的示意图.半径为R=5.0m的光滑圆形轨道固定在倾角为θ=37°的斜轨道面上的A点,圆轨道的最高点D与车(视为质点)的初始位置P点平齐,B为圆轨道的最低点,C点与圆心O等高,圆轨道与斜轨道PA之间平滑连接.小车从P点由静止开始下滑,恰好到达C点.已知g=10m/s2,sin37°=0.6,cos37°=0.8,车的质量m=100kg.求: 如图所示为汽车蓄电池与车灯 (电阻不变)、启动电动机组成的电路,蓄电池内阻为0.05Ω.电流表和电压表均为理想电表,只接通S1时,电流表示数为10A,电压表示数为12V,再接通S2,启动电动机工作时,电流表示数变为8A,则此时通过启动电动机的电流是( )
如图所示为汽车蓄电池与车灯 (电阻不变)、启动电动机组成的电路,蓄电池内阻为0.05Ω.电流表和电压表均为理想电表,只接通S1时,电流表示数为10A,电压表示数为12V,再接通S2,启动电动机工作时,电流表示数变为8A,则此时通过启动电动机的电流是( )