题目内容
如图，空间有平行于纸面的匀强电场，一带电量为-q的质点（不计重力）在电场力和某恒力的作用下沿图中虚线从静止开始沿直线从M运动到N．已知力F与MN的夹角为θ，M、N间距为d，则（ ）分析：由题，质点做直线运动，其所受的合力为零或合力方向必与速度方向在同一直线上．根据电场力做功正负，判断电势能的变化．若质点做匀速直线运动，根据题设条件F、d、θ，功的公式求出力F做功，根据动能定理，可求出电场力做功，从而求出M、N间电势差；当电场强度方向与MN垂直时，场强最小，由F=qE求出场强的最小值．
解答：解：A、若匀强电场与F方向相反，带负电的质点所受的电场力方向与F方向相同，质点的合力与MN不在同一直线上，应做曲线运动，与题不符．故A错误．
B、质点由M运动到N的过程中，电场力可能与MN的夹角为锐角，对质点做正功，电势能减小．故B错误．
C、若质点做匀速直线运动，根据动能定理得，Fdcosθ-qUMN=0，UMN=
．故C正确．
D、当电场强度方向与MN垂直时，电场力最小，最小值为Fsinθ，则场强最小值为
．故D错误．
故选C．
B、质点由M运动到N的过程中，电场力可能与MN的夹角为锐角，对质点做正功，电势能减小．故B错误．
C、若质点做匀速直线运动，根据动能定理得，Fdcosθ-qUMN=0，UMN=
| Fdcosθ |
| q |
D、当电场强度方向与MN垂直时，电场力最小，最小值为Fsinθ，则场强最小值为
| Fsinθ |
| q |
故选C．
点评：解决本题的关键知道物体做直线运动还是曲线运动的条件，以及知道电场力做功与电势能的关系．
练习册系列答案
相关题目
（2007?徐州三模）如图，在空间中有一坐标系xOy，其第一象限内充满着两个匀强磁场区域I和II，直线OP是它们的边界，区域I中的磁感应强度为B，方向垂直纸面向外；区域II中的磁感应强度为2B，方向垂直纸面向内，边界上的P点坐标为（4L，3L）．一质量为m电荷量为q的带正粒子从P点平行于y轴负方向射入区域I，经过一段时间后，粒子恰好经过原点O，忽略粒子重力，已知sin37°=0.6，cos37°=0.8．求：
（2006?广州模拟）如图所示，在空间存在这样一个磁场区域：以MN为界，上部分的匀强磁场的磁感应强度为B1，下部分的匀强磁场的磁感应强度为B2，B1=2B2=2B0，方向均垂直纸面向里，且磁场区域足够大．在距离界线为h的P点有一带负电荷的离子处于静止状态，某时刻离子分解成为带电粒子A和不带电粒子B，粒子A质量为m、带电荷q，以平行于界线MN的初速度向右运动，经过界线MN时速度方向与界线成60°角，进入下部分磁场．当粒子B沿与界线平行的直线到达位置Q点时，恰好又与粒子A相遇．不计粒子的重力．求：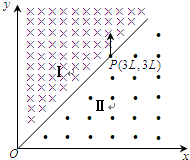
如图所示，在空间中有一坐标系oxy，其第一象限中充满着两个方向不同的匀强磁场区域Ⅰ和Ⅱ．直线OP是它们的边界．区域Ⅰ中的磁感应强度为2B，方向垂直纸面向内，区域Ⅱ中的磁感应强度为B，方向垂直纸面向外，边界上的P点坐标为（3L，3L）．一质量为m，电荷量为+q的粒子从P点平行于y轴正方向以速度v0=