题目内容
如图所示，两根不计电阻的金属导线MN与PQ 放在水平面内，MN是直导线，PQ的PQ1段是直导线，Q1Q2段是弧形导线，Q2Q3段是直导线，MN、PQ1、Q2Q3相互平行。M、P间接入一个阻值R=0.25Ω的电阻。质量m=1.0 kg、不计电阻的金属棒AB能在MN、PQ上无摩擦地滑动，金属棒始终垂直于MN，整个装置处于磁感应强度B=0.5T的匀强磁场中，磁场方向竖直向下。金属棒处于位置（I）时，给金属棒一向右的初速度v1=4 m/s，同时给一方向水平向右F1 =3 N的外力，使金属棒向右做匀减速直线运动；当金属棒运动到位置(Ⅱ)时，外力方向不变，改变大小，使金属棒向右做匀速直线运动2s到达位置(Ⅲ)。已知金属棒在位置(I)时，与MN、Q1Q2相接触于a、b两点，a、b的间距L1=1 m；金属棒在位置(Ⅱ)时，棒与MN、Q1Q2相接触于c、d两点；位置（I）到位置(Ⅱ)的距离为7.5 m。求：
（1）金属棒向右匀减速运动时的加速度大小；
（2）c、d两点间的距离L2；
（3）金属棒从位置(I)运动到位置(Ⅲ)的过程中，电阻R上放出的热量Q。
解：（1）金属棒从位置(I)到位置(Ⅱ)的过程中，加速度不变，方向向左，设大小为a，在位置I时，a、b间的感应电动势为E1，感应电流为I1，受到的安培力为F安1，则
E1=BL1 v1 （1分）
（1分）
F安1
（1分）
F安1=4 N· （1分）
根据牛顿第二定律得
F安1－F1 =ma· （1分）
a= 1 m / s2· （1分）
（2）设金属棒在位置(Ⅱ)时
速度为v2，由运动学规律得
=－2a s1
v2= 1 m / s· （2分）
由于在(I)和(II)之间做匀减速直线运动，即加速度大小保持不变，外力F1恒定，所以AB棒受到的安培力不变即F安1=F安2
· （2分）
m （2分）
（3）金属棒从位置(Ⅱ)到位置(Ⅲ)的过程中，做匀速直线运动，感应电动势大小与位置(Ⅱ)时的感应电动势大小相等，安培力与位置(Ⅱ)时的安培力大小相等，所以
F2= F安2=4 N （2分）
设位置（II）和(Ⅲ)之间的距离为s2，则
s2= v2t=2 m （1分）
设从位置(I)到位置(Ⅱ)的过程中，外力做功为W1，从位置(Ⅱ)到位置(Ⅲ)的过程中，外力做功为W2，则
W1= F1 s1=22.5 J （1分）
W2= F2 s2=8 J （1分）
根据能量守恒得W1+ W2
（2分）
解得Q = 38 J （1分）
如图所示，两根竖直固定的金属导轨ad和bc相距l=0.2m，另外两根水平金属杆MN和EF可沿导轨无摩擦地滑动，MN杆和EF杆的电阻分别为0.2Ω（竖直金属导轨的电阻不计），EF杆放置在水平绝缘平台上，回路NMEF置于匀强磁场内，磁场方向垂直于导轨平面向里，磁感应强度B=1T，试求：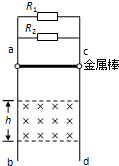
如图所示，两根电阻不计的光滑金属导轨ab、cd竖直放置，导轨间距为L，上端接有两个定值电阻R1、R2，已知R1=R2=2r．将质量为m、电阻值为r的金属棒从图示位置由静止释放，下落过程中金属棒保持水平且与导轨接触良好．自由下落一段距离后金属棒进入一个垂直于导轨平面的匀强磁场，磁场宽度为h．金属棒出磁场前R1、R2的功率均已稳定为P．则金属棒离开磁场时的速度大小为
（2013?淮安模拟）如图所示，两根等高光滑的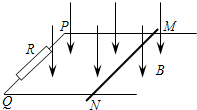
如图所示，两根光滑的平行金属导轨处于同一水平面内，相距0.3m，导轨左端PQ间用电阻R=0.2Ω相连接，导轨电阻不计，导轨上停放着一金属杆MN，杆的电阻为0.1Ω，质量为0.1kg，始终与导轨保持良好接触，整个装置处于竖直向下的匀强磁场中，磁感强度为0.5T．现对金属杆施加适当的水平力，使杆由静止开始沿导轨匀加速运动，问：
圆弧轨道，半径为r、间距为L，轨道电阻不计．在轨道顶端连有一阻值为R的电阻，整个装置处在一竖直向上的匀强磁场中，磁感应强度为B.现有一根长度稍大于L、质量为m、电阻不计的金属棒从轨道的顶端ab处由静止开始下滑，到达轨道底端cd时受到轨道的支持力为2mg．整个过程中金属棒与导轨电接触良好，求：