题目内容
8.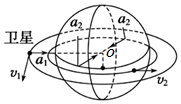 如图所示,同步卫星离地心O 的距离为 r,运行速率为v1,加速度为a1;地球赤道上的物体随地球自转的加速度为a2;第一宇宙速度为v2;地球的质量为M,半径为R,赤道处的重力加速度为g.万有引力常数为G,则下列比值正确的是( )
如图所示,同步卫星离地心O 的距离为 r,运行速率为v1,加速度为a1;地球赤道上的物体随地球自转的加速度为a2;第一宇宙速度为v2;地球的质量为M,半径为R,赤道处的重力加速度为g.万有引力常数为G,则下列比值正确的是( )| A. | $\frac{{a}_{1}}{{a}_{2}}$=($\frac{R}{r}$)2 | B. | $\frac{{a}_{1}}{g}$=$\frac{1}{1}$ | C. | $\frac{{a}_{2}}{g}$=$\frac{GM}{g{R}^{2}}$-1 | D. | $\frac{{v}_{1}}{{v}_{2}}$=$\frac{r}{R}$ |
分析 第一宇宙速度即为近地卫星的环绕速度.
同步卫星和近地卫星都绕地球做匀速圆周运动,根据万有引力提供向心力去求两卫星的线速度之比.
同步卫星与地球赤道上的物体具有相同的角速度,根据a=rω2,去求两者的向心加速度之比
解答 解:A、因为地球同步卫星的角速度和地球赤道上的物体随地球自转的角速度相同,
由a1=ω2R,a2=ω2r可得,$\frac{{a}_{1}}{{a}_{2}}=\frac{r}{R}$,故A错误.
B、对于地球同步卫星和以第一宇宙速度运动的近地卫星,由万有引力提供做匀速圆周运动所需向心力得到:
ma1=$\frac{GMm}{{r}^{2}}$
在地球的表面,重力近似等于万有引力,则:mg=$\frac{GMm}{{R}^{2}}$
所以:$\frac{{a}_{1}}{g}=\frac{{R}^{2}}{{r}^{2}}$.故B错误;
C、在赤道处,物体受到的万有引力的一部分提供向心力,则:ma2=$\frac{GMm}{{R}^{2}}$-mg
所以:$\frac{{a}_{2}}{g}=\frac{GM}{g{R}^{2}}$-1.故C正确;
D、由万有引力提供向心力得:$\frac{GmM}{{r}^{2}}$=m$\frac{{v}^{2}}{r}$
v=$\sqrt{\frac{GM}{r}}$,M为地球质量,r为轨道半径.得$\frac{{v}_{1}}{{v}_{2}}=\sqrt{\frac{R}{r}}$,故D错误.
故选:C
点评 求一个物理量之比,我们应该把这个物理量先用已知的物理量表示出来,再进行之比.
解决本题的关键掌握万有引力提供向心力以及知道同步卫星与地球赤道上的物体具有相同的角速度.

练习册系列答案
 超能学典应用题题卡系列答案
超能学典应用题题卡系列答案
相关题目
13.关于光谱的下列说法中,正确的是( )
| A. | 用光栅或棱镜的色散作用,可以把光按波长展开,获得光的波长和强度分布的纪录叫光谱 | |
| B. | 氢光谱证实了玻尔提出的“原子核的能级量子化的假说” | |
| C. | 白炽灯和霓虹灯光的光谱是明线光谱,都能用来做光谱分析 | |
| D. | 太阳光谱是吸收光谱,其中的暗线说明太阳的内部存在着与这些暗线对相应的元素 |
14.某同学将质量为4kg的铅球,以6m/s的速度投出,铅球在出手时的动能是( )
| A. | 12J | B. | 24J | C. | 72J | D. | 144J |
13.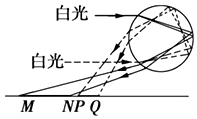 虹和霓是太阳光在水珠内分别经过一次和两次反射后出射形成的,可用白光照射玻璃球来说明.两束平行白光照射到透明玻璃球后,在水平的白色桌面上会形成MN和PQ两条彩色光带,光路如图8所示.关于照到M、N、P、Q点的单色光的说法中正确的是( )
虹和霓是太阳光在水珠内分别经过一次和两次反射后出射形成的,可用白光照射玻璃球来说明.两束平行白光照射到透明玻璃球后,在水平的白色桌面上会形成MN和PQ两条彩色光带,光路如图8所示.关于照到M、N、P、Q点的单色光的说法中正确的是( )
 虹和霓是太阳光在水珠内分别经过一次和两次反射后出射形成的,可用白光照射玻璃球来说明.两束平行白光照射到透明玻璃球后,在水平的白色桌面上会形成MN和PQ两条彩色光带,光路如图8所示.关于照到M、N、P、Q点的单色光的说法中正确的是( )
虹和霓是太阳光在水珠内分别经过一次和两次反射后出射形成的,可用白光照射玻璃球来说明.两束平行白光照射到透明玻璃球后,在水平的白色桌面上会形成MN和PQ两条彩色光带,光路如图8所示.关于照到M、N、P、Q点的单色光的说法中正确的是( )| A. | M、N、P、Q点的光的颜色分别为紫、红、红、紫 | |
| B. | M点的光的波动性较N点的光更显著 | |
| C. | 在同一单缝衍射装置上做实验,用P点的光得到的衍射图样的中央明纹宽度较Q点的光更窄 | |
| D. | 水中相同深度处有两个光源,其颜色分别与P、Q两点的光同色,在其正上方的水面之上,同等条件下观测,同P色的点光源在水下的像最深,且其照亮水面的面积最大 |
20.飞艇在平流层飞行的全过程中受到的合力( )
| A. | 恒为零 | B. | 总是做正功 | C. | 总是做负功 | D. | 做的总功为零 |
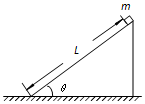 如图所示,倾角为θ=37°的光滑斜面固定在地面上,斜面的长度为L=3.0m;质量m=0.10kg的滑块(可视为质点)从斜面顶端由静止滑下;已知sin37°=0.60,cos37°=0.80,空气阻力可忽略不计,重力加速度g取10m/s2.求:
如图所示,倾角为θ=37°的光滑斜面固定在地面上,斜面的长度为L=3.0m;质量m=0.10kg的滑块(可视为质点)从斜面顶端由静止滑下;已知sin37°=0.60,cos37°=0.80,空气阻力可忽略不计,重力加速度g取10m/s2.求: 如图所示,摩托车做腾跃特技衰演,摩托车关闭发动机后以v0=10m/s的初速度冲上高为h、顶部水平的高台.然后从高台水平飞出,在各种阻力的影响可以忽略不计的情况下,试分析当台高h多大时,飞出的水平距离最远?最远距离是多少?
如图所示,摩托车做腾跃特技衰演,摩托车关闭发动机后以v0=10m/s的初速度冲上高为h、顶部水平的高台.然后从高台水平飞出,在各种阻力的影响可以忽略不计的情况下,试分析当台高h多大时,飞出的水平距离最远?最远距离是多少?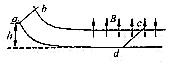 如图所示,宽为l、光滑的导电轨道的弧形部分处于磁场外,轨道的水平部分处于垂直轨道平面向上、磁感强度为B的匀强磁场中,质量为2m的金属杆cd静止在水平轨道上,另一质量为m的金属杆ab,从弧形轨道上h高处由静止开始下滑.设ab杆和cd杆始终与轨道垂直,且接触良好,ab杆与cd杆不会相碰,ab和cd杆的电阻均为R,轨道电阻不计.求:
如图所示,宽为l、光滑的导电轨道的弧形部分处于磁场外,轨道的水平部分处于垂直轨道平面向上、磁感强度为B的匀强磁场中,质量为2m的金属杆cd静止在水平轨道上,另一质量为m的金属杆ab,从弧形轨道上h高处由静止开始下滑.设ab杆和cd杆始终与轨道垂直,且接触良好,ab杆与cd杆不会相碰,ab和cd杆的电阻均为R,轨道电阻不计.求: