Question

16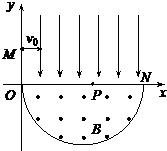．如图，在平面直角坐标系xOy内，第Ⅰ象限存在沿y轴负方向的匀强电场，第Ⅳ象限以ON为直径的半圆形区域内，存在垂直于坐标平面向外的匀强磁场，磁感应强度为B，一质量为m、电荷量为q的带正电的粒子，从y轴正半轴上y=h处的M点，以速度V₀垂直于y轴射入电场，经x轴上x=2h处的P点进入磁场，最后以垂直于y轴的方向射出磁场．不计粒子重力．求
（1）电场强度大小E；
（2）粒子从进入电场到离开磁场经历的总时间t．

Answer 1

分析 （1）电场中做类似平抛运动，根据类平抛运动的水平分位移公式和竖直分位移公式以及牛顿第二定律列式求出电场强度；
（2）先求解出类似平抛运动的时间，然后根据几何关系得到圆弧的圆心角，最后根据周期公式求解出圆周运动的时间，最后得到总时间．

解答 解：（1）设粒子在电场中运动的时间为t₁，
x方向：2h=v₀t₁
y方向：h=$\frac{1}{2}$at₁²
根据牛顿第二定律：Eq=ma，
联立以上三式，解得：E=$\frac{m{v}_{0}^{2}}{2qh}$；
（2）粒子在电场中运动的时间：t₁=$\frac{2h}{{v}_{0}}$，
粒子在磁场中运动的周期：T=$\frac{2πm}{qB}$，
根据粒子入射磁场时与x轴成45°，射出磁场时垂直于y轴，
可求出粒子在磁场中运动的圆弧所对的圆心角为θ=135°．
故粒子在磁场中运动的时间为：t₂=$\frac{θ}{360°}$T=$\frac{135°}{360°}$×$\frac{2πm}{qB}$=$\frac{3πm}{4qB}$，
粒子的运动时间：t=t₁+t₂=$\frac{2h}{{v}_{0}}$+$\frac{3πm}{4qB}$；
答：（1）电场强度大小E为$\frac{m{v}_{0}^{2}}{2qh}$；
（2）粒子从进入电场到离开磁场经历的总时间t为：$\frac{2h}{{v}_{0}}$+$\frac{3πm}{4qB}$．

点评 本题考查了粒子在匀强电场与匀强磁场中的运动，考查了求电场强度与粒子的运动时间，本题的解题关键是明确粒子的运动，画出轨迹，然后结合几何关系，分为类似平抛运动和匀速圆周运动进行分析计算．