题目内容
13.电磁感应式无线充电的工作原理如图1所示,由送电线圈和受电线圈组成.某兴趣小组在模拟研究时,受电线圈的匝数为n=50匝,面积S=0.02m2,电阻r=1.0Ω,在它的两端接一只电阻R=9.0Ω的小灯泡如图(甲)所示.假设在受电线圈内存在与线圈平面垂直的磁场均匀分布,其磁感应强度随时间按图(乙)所示的规律变化,受电线圈中产生的感应电动势瞬时值的表达式e=nBmS$\frac{2π}{T}$cos$\frac{2π}{T}$t,其中Bm为磁感应强度的最大值,T为磁场变化的周期,不计灯丝电阻随温度的变化.求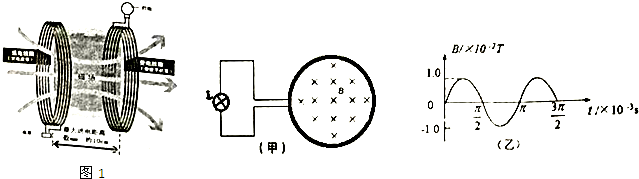
(1)线圈中产生感应电动势的最大值;
(2)小灯泡消耗的电功率;
(3)在磁感应强度变化的$\frac{T}{4}$-$\frac{3T}{4}$的时间内,通过小灯泡的电荷量.
分析 (1)根据受电线圈中产生的感应电动势瞬时值的表达式,知感应电动势的最大值${E}_{m}^{\;}=n{B}_{m}^{\;}S\frac{2π}{T}$,代入数据求出最大值;
(2)求出电路中电流的最大值和有效值,根据$P={I}_{\;}^{2}R$求出小灯泡消耗的电功率;
(3)求出平均感应电动势和平均电流,根据$Q=\overline{I}•△t$求通过灯泡的电荷量
解答 解:(1)由图象可知周期为$T=π×1{0}_{\;}^{-3}s$,${B}_{m}^{\;}=1×1{0}_{\;}^{-2}T$
线圈中感应电动势的最大值${E}_{m}^{\;}=n{B}_{m}^{\;}S\frac{2π}{T}=20V$
(2)电路中电流的最大值为${I}_{m}^{\;}=\frac{{E}_{m}^{\;}}{R+r}=2A$
通过小灯泡电流的有效值为$I=\frac{{I}_{m}^{\;}}{\sqrt{2}}=\sqrt{2}A$
小灯泡消耗的电功率为$P={I}_{\;}^{2}R=18W$
(3)线圈中感应电动势的平均值$\overline{E}=nS\frac{△B}{△t}$
通过灯泡的平均电流$\overline{I}=\frac{\overline{E}}{R+r}$
通过灯泡的电荷量$Q=\overline{I}t$
由上述三式可得$Q=nS\frac{△B}{R+r}=2×1{0}_{\;}^{-3}C$
答:(1)线圈中产生感应电动势的最大值20V;
(2)小灯泡消耗的电功率18W;
(3)在磁感应强度变化的$\frac{T}{4}$-$\frac{3T}{4}$的时间内,通过小灯泡的电荷量$2×1{0}_{\;}^{-3}C$
点评 求解交变电流的电功率时要用有效值.在电磁感应中通过导体截面的电量经验公式是Q=n$\frac{△Φ}{R+r}$,可以在推导的基础上记住.

 如图所示电路,R1、R2、R3是定值电阻,c点接地,a、b两接线柱接上直流电源,开关S是断开的,那么,当开关S闭合后( )
如图所示电路,R1、R2、R3是定值电阻,c点接地,a、b两接线柱接上直流电源,开关S是断开的,那么,当开关S闭合后( )| A. | ab两点电势均升高 | B. | ab两点电势均降低 | ||
| C. | a点电势升高,b点电势降低 | D. | a点电势降低,b点电势升高 |
 如图所示,虚线a、b、c代表电场中的三个等势面,相邻等势面间的电势差相等,实线为一带正电的质点仅在电场力作用下的运动轨迹,P、Q是这条轨迹上的两点,据此可知( )
如图所示,虚线a、b、c代表电场中的三个等势面,相邻等势面间的电势差相等,实线为一带正电的质点仅在电场力作用下的运动轨迹,P、Q是这条轨迹上的两点,据此可知( )| A. | 三个等势面中,c的电势较高 | B. | 带电质点通过Q点时的电势能较大 | ||
| C. | 带电质点通过P点时的动能较大 | D. | 带电质点通过Q点时的加速度较大 |
 如图所示,质量为m的物体,在水平外力F作用下,以速度v沿水平面匀速运动,当物体运动到A点时撤去外力F,物体由A点继续向前滑行的过程中经过B点,则物体由A点到B点的过程中,下列说法正确的是( )
如图所示,质量为m的物体,在水平外力F作用下,以速度v沿水平面匀速运动,当物体运动到A点时撤去外力F,物体由A点继续向前滑行的过程中经过B点,则物体由A点到B点的过程中,下列说法正确的是( )| A. | v越大,摩擦力对物体的冲量越大;摩擦力做功越多 | |
| B. | v越大,摩擦力对物体的冲量越大;摩擦力做功与v的大小无关 | |
| C. | v越大,摩擦力对物体的冲量越小;摩擦力做功越少 | |
| D. | v越大,摩擦力对物体的冲量越小;摩擦力做功与v的大小无关 |
 一足够长的粗细均匀的杆被一细绳吊于高处,杆下端离地面高H,上端套一个细环,如图所示.断开轻绳,杆和环自由下落,假设杆与地面发生碰撞时触地时间极短,无动能损失,杆立即获得等大反向的速度.已知杆和环的质量均为m,相互间最大静摩擦力等于滑动摩擦力kmg(重力加速度为g,
一足够长的粗细均匀的杆被一细绳吊于高处,杆下端离地面高H,上端套一个细环,如图所示.断开轻绳,杆和环自由下落,假设杆与地面发生碰撞时触地时间极短,无动能损失,杆立即获得等大反向的速度.已知杆和环的质量均为m,相互间最大静摩擦力等于滑动摩擦力kmg(重力加速度为g,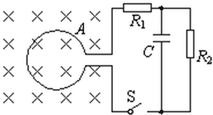 横截面积S=0.2m2、n=100匝的圆形线圈A处在如图所示的磁场内,磁感应强度变化率为0.02T/s.开始时S未闭合,R1=3Ω,R2=6Ω,C=30 μF,线圈内阻1Ω,求:
横截面积S=0.2m2、n=100匝的圆形线圈A处在如图所示的磁场内,磁感应强度变化率为0.02T/s.开始时S未闭合,R1=3Ω,R2=6Ω,C=30 μF,线圈内阻1Ω,求: 如图所示,匀强磁场中有一矩形闭合线圈abcd,线圈平面与磁场垂直.已知线圈的匝数N=100,边长ab=1.0m、bc=0.5m,电阻r=2Ω,磁感应强度B在0~1s内从零均匀变化到0.2T.在1~5s内从0.2T均匀变化到-0.2T,取垂直纸面向里为磁场的正方向.求:
如图所示,匀强磁场中有一矩形闭合线圈abcd,线圈平面与磁场垂直.已知线圈的匝数N=100,边长ab=1.0m、bc=0.5m,电阻r=2Ω,磁感应强度B在0~1s内从零均匀变化到0.2T.在1~5s内从0.2T均匀变化到-0.2T,取垂直纸面向里为磁场的正方向.求:
