题目内容
3. 一足够长的粗细均匀的杆被一细绳吊于高处,杆下端离地面高H,上端套一个细环,如图所示.断开轻绳,杆和环自由下落,假设杆与地面发生碰撞时触地时间极短,无动能损失,杆立即获得等大反向的速度.已知杆和环的质量均为m,相互间最大静摩擦力等于滑动摩擦力kmg(重力加速度为g,
一足够长的粗细均匀的杆被一细绳吊于高处,杆下端离地面高H,上端套一个细环,如图所示.断开轻绳,杆和环自由下落,假设杆与地面发生碰撞时触地时间极短,无动能损失,杆立即获得等大反向的速度.已知杆和环的质量均为m,相互间最大静摩擦力等于滑动摩擦力kmg(重力加速度为g,k>1).杆在整个过程中始终保持竖直,空气阻力不计.求:
(1)杆第一次与地面碰撞弹起上升的过程中,环的加速度
(2)杆与地面第二次碰撞前的瞬时速度
(3)从断开轻绳到杆和环静止,摩擦力对环和杆做的总功.
分析 (1)在杆上升的过程中,环要受到重力的作用,同时由于环向下运动而棒向上运动,环还要受到杆的向上的摩擦力的作用,根据牛顿第二定律列式可以求得加速度的大小;
(2)根据动能定理求出杆第一次落地的速度大小,然后根据顿第二定律求出杆弹起后的加速度,最后根据运动学公式可以求得杆与地面第二次碰撞前的瞬时速度;
(3)整个过程中能量的损失都是由于摩擦力对物体做的功,所以根据能量的守恒可以较简单的求得摩擦力对环和杆做的总功.
解答 解:(1)设杆第一次上升的过程中环的加速度为a,
根据牛顿第二定律可得,kmg-mg=ma,
解得:a=(k-1)g,方向竖直向上.
(2)杆第一次落地的速度大小为v1,
由动能定理得,2mgH=$\frac{1}{2}$2m${v}_{1}^{2}$-0,
解得:v1=$\sqrt{2gH}$,
杆弹起后的加速度为a′,
根据牛顿第二定律可得,mg+kmg=ma′,
解得:a′=(k+1)g,方向竖直向下,
从落地经时间t1达到共同速度,
则有:v1-at1=-v1+a′t1,
解得:t1=$\frac{2{v}_{1}}{a+{a}^{′}}$=$\frac{2{v}_{1}}{(k-1)g+(k+1)g}$=$\frac{{v}_{1}}{kg}$,
共同速度为:${v}_{1}^{′}$=v1-at1=v1-(k-1)g×$\frac{{v}_{1}}{kg}$=$\frac{{v}_{1}}{k}$,
杆上升的高度:h1=v1t1-$\frac{1}{2}$a′${t}_{1}^{2}$=$\frac{(k-1)H}{{k}^{2}}$,
所以杆第二次落地时的速度:
v2=$\sqrt{v{′}_{1}^{2}+2g{h}_{1}}$=$\sqrt{\frac{2gH}{k}}$,方向竖直向下.
(3)经过足够长的时间杆和环最终静止,
设这一过程中它们相对滑动的总路程为l,
由能量的转化和守恒定律有:
mgH+mg(H+l)=kmgl,
解得:l=$\frac{2H}{k-1}$,
则摩擦力对环和棒做的总功:
W=-kmgl=-$\frac{2kmgH}{k-1}$.
答:(1)环的加速度为(k-1)g,方向竖直向上;
(2)杆与地面第二次碰撞前的瞬时速度为$\sqrt{\frac{2gH}{k}}$,方向竖直向下;
(3)从断开轻绳到杆和环静止,摩擦力对环和杆做的总功为-$\frac{2kmgH}{k-1}$.
点评 本题考查功能关系以及牛顿第二定律的综合应用,属于力学综合问题,注意:求摩擦力总功应用能量的守恒来解决本题可以很简单的求出结果,
这样既能够简化解题的过程还可以节约宝贵的时间,所以在平时一定要考虑如何解题能够简单快捷.

| A. | α粒子流 | B. | 质子流 | C. | 中子流 | D. | 电子流 |
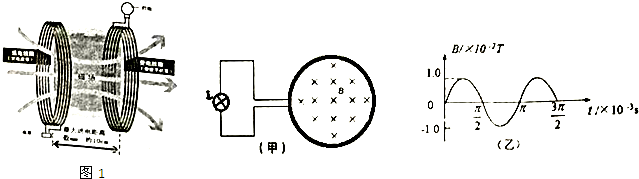
 如图表示磁流体的发电原理:将一束等离子体(重力不计)沿图示方向以速度v喷射入磁场,金属板A、B就形成一个直流电源,设磁感应强度为B,金属板A、B相距d,外接电阻R,A、B间弥漫的电离气体电阻为r.则下述说法正确的是( )
如图表示磁流体的发电原理:将一束等离子体(重力不计)沿图示方向以速度v喷射入磁场,金属板A、B就形成一个直流电源,设磁感应强度为B,金属板A、B相距d,外接电阻R,A、B间弥漫的电离气体电阻为r.则下述说法正确的是( )| A. | 金属板A为电源的正极 | |
| B. | 开关断开时,金属板间的电势差为Bvd | |
| C. | 开关闭合后,金属板间的电势差为$\frac{BvdR}{R+r}$ | |
| D. | 等离子体发生偏转的原因是洛伦兹力大于所受电场力 |
 如图所示,A、B为两块平行金属板,板长为l,两板间的距离为d,且d<<l,B板接地,A板的电势U可随时间发生突变,质量为m、电量为q的带正电粒子,从A的边缘贴近A板以平行于A板的初速度v0射入两板间的空间中,这时U=U0>0;经过一段时间t1,U突变为U=-U0;再经过一段时间t2,U又突变为U=U0;再经过一段时间t3,粒子又贴近A板且沿平行于A板的方向从A板的另一边缘处以速度v0射出两板间的空间,已知粒子在运动过程中曾非常接近B板但恰好没有B板接触,不计重力,则( )
如图所示,A、B为两块平行金属板,板长为l,两板间的距离为d,且d<<l,B板接地,A板的电势U可随时间发生突变,质量为m、电量为q的带正电粒子,从A的边缘贴近A板以平行于A板的初速度v0射入两板间的空间中,这时U=U0>0;经过一段时间t1,U突变为U=-U0;再经过一段时间t2,U又突变为U=U0;再经过一段时间t3,粒子又贴近A板且沿平行于A板的方向从A板的另一边缘处以速度v0射出两板间的空间,已知粒子在运动过程中曾非常接近B板但恰好没有B板接触,不计重力,则( )| A. | t1=$\frac{l}{4{v}_{0}}$ | B. | t2=$\frac{l}{2{v}_{0}}$ | ||
| C. | U0=$\frac{8{mv}_{0}^{2}{d}^{2}}{q{l}^{2}}$ | D. | U0=$\frac{16{mv}_{0}^{2}{d}^{2}}{q{l}^{2}}$ |
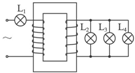 如图所示,一理想变压器的变压比为3:1,图中四只灯泡完全相同.在L1、L2、L3仍然发光的条件下,若没有L4,则( )
如图所示,一理想变压器的变压比为3:1,图中四只灯泡完全相同.在L1、L2、L3仍然发光的条件下,若没有L4,则( )| A. | L1、L2、L3变亮 | B. | L1、L2、L3变暗 | ||
| C. | L1变亮,L2、L3变暗 | D. | L1变暗,L2、L3亮度变亮 |

 高中电学实验的核心是测电阻,当然所测的对象是不同的,有灯泡的电阻、电阻丝的电阻、电表的电阻、电源的电阻等;所有的方法也不同,有伏安法、半偏法、等效代替法等,其中最常用的是伏安法,测量电路如图所示.
高中电学实验的核心是测电阻,当然所测的对象是不同的,有灯泡的电阻、电阻丝的电阻、电表的电阻、电源的电阻等;所有的方法也不同,有伏安法、半偏法、等效代替法等,其中最常用的是伏安法,测量电路如图所示.