题目内容
12.一个质点沿直线到A点时,速度为3m/s,然后匀加速运动到B点时,速度为12m/s历时6s,到B点后,又匀减速运动,再经6s到达C点,并停下来,求(1)A到B点的过程中加速度的大小.
(2)从B点到C点的位移.
分析 (1)质点从A到B做匀加速运动,已知初速度为3m/s,末速度为12m/s,运动时间为6s,由加速度的定义式求解加速度.
(2)质点从B到C做减速运动,初速度为12m/s,末速度为零,由位移-速度公式即可求出.
解答 解:设质点运动方向为正方向
(1)质点从A到B做匀加速运动,初速度为v0=3m/s,末速度为v=12m/s,运动时间为t=6s,
则加速度为${a}_{1}=\frac{v-{v}_{0}}{t}$=$\frac{12-3}{6}=1.5$m/s2
(2)质点从B到C做减速运动,初速度为v0′=12m/s,末速度为v′=0,时间是6s,由平均速度公式得:.
x=$\frac{{v}_{0}′+0}{2}•t$=$\frac{12+0}{2}×6=36$m
答:(1)A到B点的过程中加速度的大小是1.5m/s2.
(2)从B点到C点的位移是36m.
点评 本题是两个运动过程的问题,要抓住前后两个过程的联系,基本联系是:前一过程的末速度是后一过程的初速度.注意加速度的大小是加速度的绝对值.

练习册系列答案
相关题目
3.有两个共点力,F1=2N,F2=4N,合力大小可能是( )
| A. | 1N | B. | 2N | C. | 5N | D. | 7N |
20. 甲、乙两车某时刻由同一地点沿同一方向开始做直线运动,若以该时刻为计时起点,得到两车的位移-时间图象如图所示,则下列说法正确的是( )
甲、乙两车某时刻由同一地点沿同一方向开始做直线运动,若以该时刻为计时起点,得到两车的位移-时间图象如图所示,则下列说法正确的是( )
 甲、乙两车某时刻由同一地点沿同一方向开始做直线运动,若以该时刻为计时起点,得到两车的位移-时间图象如图所示,则下列说法正确的是( )
甲、乙两车某时刻由同一地点沿同一方向开始做直线运动,若以该时刻为计时起点,得到两车的位移-时间图象如图所示,则下列说法正确的是( )| A. | t1时刻甲车从后面追上乙车 | |
| B. | t1时刻两车相距最远 | |
| C. | t1时刻两车的速度刚好相等 | |
| D. | 0至t1时间内,乙车的平均速度小于甲车的平均速度 |
7. 半圆柱体P放在粗糙的水平地面上,其右端有竖直挡板MN.在P和MN之间放有一个光滑均匀的小圆柱体Q,整个装置处于静止状态.如图所示是这个装置的纵截面图.若用外力使MN保持竖直并缓慢地向右移动,在Q落到地面以前,发现P始终保持静止.在此过程中,下列说法中正确的是( )
半圆柱体P放在粗糙的水平地面上,其右端有竖直挡板MN.在P和MN之间放有一个光滑均匀的小圆柱体Q,整个装置处于静止状态.如图所示是这个装置的纵截面图.若用外力使MN保持竖直并缓慢地向右移动,在Q落到地面以前,发现P始终保持静止.在此过程中,下列说法中正确的是( )
 半圆柱体P放在粗糙的水平地面上,其右端有竖直挡板MN.在P和MN之间放有一个光滑均匀的小圆柱体Q,整个装置处于静止状态.如图所示是这个装置的纵截面图.若用外力使MN保持竖直并缓慢地向右移动,在Q落到地面以前,发现P始终保持静止.在此过程中,下列说法中正确的是( )
半圆柱体P放在粗糙的水平地面上,其右端有竖直挡板MN.在P和MN之间放有一个光滑均匀的小圆柱体Q,整个装置处于静止状态.如图所示是这个装置的纵截面图.若用外力使MN保持竖直并缓慢地向右移动,在Q落到地面以前,发现P始终保持静止.在此过程中,下列说法中正确的是( )| A. | MN对Q的弹力逐渐减小 | B. | 地面对P的摩擦力逐渐增大 | ||
| C. | P、Q间的弹力先减小后增大 | D. | Q受到P和MN的合力逐渐增大 |
17. 小球沿足够长的斜面向上做匀减速运动,依次经a、b、c、d到达最高点e.已知ab=bd=6m,bc=1m,小球从a到c和从c到d所用的时间都是2s,设小球经b、c时的速度分别为vb、vc,则( )
小球沿足够长的斜面向上做匀减速运动,依次经a、b、c、d到达最高点e.已知ab=bd=6m,bc=1m,小球从a到c和从c到d所用的时间都是2s,设小球经b、c时的速度分别为vb、vc,则( )
 小球沿足够长的斜面向上做匀减速运动,依次经a、b、c、d到达最高点e.已知ab=bd=6m,bc=1m,小球从a到c和从c到d所用的时间都是2s,设小球经b、c时的速度分别为vb、vc,则( )
小球沿足够长的斜面向上做匀减速运动,依次经a、b、c、d到达最高点e.已知ab=bd=6m,bc=1m,小球从a到c和从c到d所用的时间都是2s,设小球经b、c时的速度分别为vb、vc,则( )| A. | vb=$\sqrt{10}$m/s | B. | vc=3m/s | ||
| C. | de=3m | D. | 从d到e所用时间为4s |

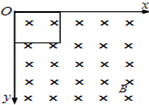 如图所示,一边长为L、质量为m、电阻为R的正方形金属框竖直放置在磁场中,磁场方向垂直方框平面,磁感应强度的大小随y的变化规律为B=B0+ky(k为恒定常数且大于零),同一水平面上磁感应强度相同.现将方框从y=0处自由下落,重力加速度为g,设磁场区域足够大,不计空气阻力,则方框中感应电流的方向为逆时针(选填“顺时针”或“逆时针”),方框最终运动的速度大小为$\frac{mgR}{{k}^{2}{L}^{4}}$.
如图所示,一边长为L、质量为m、电阻为R的正方形金属框竖直放置在磁场中,磁场方向垂直方框平面,磁感应强度的大小随y的变化规律为B=B0+ky(k为恒定常数且大于零),同一水平面上磁感应强度相同.现将方框从y=0处自由下落,重力加速度为g,设磁场区域足够大,不计空气阻力,则方框中感应电流的方向为逆时针(选填“顺时针”或“逆时针”),方框最终运动的速度大小为$\frac{mgR}{{k}^{2}{L}^{4}}$.